|
INTRODUCCIÓN
En realidad, lo que se esconde detrás de el largo título que encabeza este texto intenta ser una exposición, lo más sencilla posible, de los fundamentos físicos y matemáticos de un gran número de fenómenos con los que nos encontramos en la vida cotidiana.
La cantidad de luz que refleja, transmite y absorbe el vidrio de nuestras ventanas, la pantalla de nuestro televisor o de nuestro ordenador, las reflexiones coloreadas en charcos de agua manchados con aceite o grasa, o la coloración de los cristales con capa antireflectante de nuestras gafas, no son sino unos pocos ejemplos de situaciones que observamos a menudo y cuya explicación no siempre nos resulta fácil encontrar.
Nos gustaría saber por qué unas pantallas de televisión reflejan mayor cantidad de luz que otras, o cual es la razón por la que la distancia y la posición de los objetos y seres que se encuentran bajo el agua se nos presenta alterada con respecto a las que percibiríamos fuera de ella.
Estas y otras muchas observaciones nos son familiares y otras, aunque quizá menos, se producen en multitud de situaciones como por ejemplo en la cantidad de luz que es reflejada y absorbida en colectores y paneles de energía solar, o los efectos de producción de espejismos en desiertos y en carreteras de asfalto sometidos a altas temperaturas.
Todas ellas tienen algo en común, son fenómenos en los que interviene la luz y algún tipo de superficie o interfase de transición entre dos medios materiales diferentes, superficie que es plana y en la cual la luz se refleja y transmite dando lugar a toda esa serie de efectos, dependiendo de las características de la luz que interviene, de las propiedades del medio o medios implicados y del número y cualidades de las superficies que delimitan esos medios materiales.
Poder entender por qué no podremos broncearnos si tomamos el Sol detrás del vidrio de la ventana de nuestra casa o automóvil, o por qué necesitamos usar gafas de bucear para poder ver bien debajo del agua, es motivo de satisfacción y al mismo tiempo equipaje cultural que nos ayudará a mejorar nuestras condiciones de vida.
Una sencilla explicación puede ser suficiente y adecuada en muchos casos para comprender estos fenómenos, pero en este texto se busca además una respuesta más completa, que incluya también un tratamiento matemático de los temas, con la obtención de fórmulas y expresiones que permitan cuantificar y predecir los fenómenos y su magnitud mediante simulaciones y su comparación con mediciones experimentales que corroboren las previsiones realizadas.
La aproximación al fenómeno de la luz que aquí se adopta es la de considerarla como una onda electromagnética, sin que por ello debamos olvidar su carácter de "cuanto" o corpúsculo que se pone de manifiesto en determinadas situaciones.
Por ello, las expresiones y fórmulas que se deriven lo serán a partir de la teoría electromagnética clásica que proporciona cobertura suficiente y con la que se obtienen resultados satisfactorios para el tipo de fenómenos que aquí se verán.
En lo relativo a la obtención de algunas expresiones matemáticas sólo se hará referencia a los resultados finales, sin detenerse en las operaciones para su deducción, resultados que por otra parte están bien contrastados y recogidos en multitud de publicaciones, por lo que su deducción matemática sólo acarrearía mayor lentitud y complejidad en el progreso hacia la comprensión de los mecanismos físicos de los fenómenos descritos.
A pesar de ello, cierto grado de formalismo matemático es inevitable y por ello el lector que no se encuentre familiarizado con algunos conceptos del álgebra y cálculo matemáticos, puede experimentar algo de dificultad en la comprensión de varias de las expresiones y ecuaciones.
Mi recomendación en ese caso sería que intente progresar ignorando en la medida de lo posible tales expresiones, reteniendo sólo los conceptos y consecuencias físicas que junto con ellas se extraen, pues al final los cálculos se podrán hacer con un ordenador, computador, o calculadora y lo que tendremos que saber es proporcionarle los datos de partida que se necesitan para dichos cálculos y que dependerán de las características físicas del problema que manejemos.
Sólo una cuestión más y es sobre la notación empleada en las expresiones matemáticas utilizadas, en las que se ha intentado mantener de forma coherente las mismas denominaciones de los distintos parámetros a lo largo de todo el texto para evitar la confusión que con frecuencia se produce en muchos libros de texto y publicaciones, en las que sucesivamente se van designando a diferentes conceptos con las mismas letras y símbolos produciendo así una dificultad añadida que aquí he intentado evitar.
Como ejemplo de esto se verá que el vector de propagación de la onda que se nombra desde el principio con la letra griega g en lugar de la más corrientemente utilizada, k , se mantiene con esa denominación para evitar confusiones cuando luego se introduzcan los coeficientes dieléctricos ke y la componente imaginaria del índice de refracción, que también suele designarse por la letra k.

EL CAMPO ELECTROMAGNÉTICO
La luz es una perturbación electromagnética oscilatoria que tiene su origen en una alteración energética de un medio material y se propaga por el espacio o por los medios materiales que se interponen en su camino.
A diferencia de otros tipos de perturbaciones oscilatorias, como las ondas de presión del sonido o las oscilaciones en una cuerda de guitarra, la luz tiene la particularidad de que no necesita de un medio material para propagarse ya que se ha comprobado que se propaga también en el espacio vacio.
Sí precisa, hasta donde sabemos, de un medio material para originarse, ya sea un cuerpo caliente o incandescente o un material que ha sido previamente excitado a estados superiores de energía y vuelve a su estado de equilibrio emitiendo radiación.
Al ser una perturbación electromagnética del medio, esto significa que se puede poner de manifiesto la existencia de un cierto campo eléctrico y campo magnético en cualquier punto de ese medio que se encuentre situado en la trayectoria por la que la luz se propaga.
Para poner de manifiesto su existencia habrá que realizar algún tipo de medida o detección de algún fenómeno inducido por la presencia de dichos campos y para ello tenemos que introducir algún elemento material, por eso suponemos que la luz se propaga en el vacío porque somos capaces de detectarla después de que se haya interpuesto un espacio vacio entre la fuente donde se origina y el punto donde la detectamos, no porque seamos capaces de demostrar su existencia en un espacio que está estrictamente vacio.
Para encontrar una expresión matemática que describa los campos eléctrico y magnético de esta perturbación se suelen tomar como punto de partida las ecuaciones de Maxwell, ecuaciones empíricas basadas en las observaciones experimentales realizadas hasta el momento (1873) en que Maxwell las formuló como una generalización de dichas observaciones.
Son cuatro y se pueden expresar de la siguiente forma:
rot H = J +  D/ D/ t t
rot E = -  B/ B/ t t
div D = r
div B = 0
Su descripción detallada se puede encontrar en cualquier libro o texto de electromagnetismo de grado medio (3) y en ellas se plantean las condiciones que cumplen los vectores campo eléctrico, E, y campo magnético, B, y sus vectores asociados, el desplazamiento eléctrico, D, y la intensidad magnética, H, en función del tiempo, t, la densidad de carga eléctrica libre, r, y la densidad de corriente eléctrica circulante, J.
En ellas, rot y div designan a los operadores matemáticos rotacional y divergencia, respectivamente y, si el medio de propagación es lineal, entre E y D y entre B y H existen las relaciones:
D = e . E ,, B = m . H , y además se verifica que J = s . E , siendo s la conductividad eléctrica del medio y siendo e y m dos parámetros que se denominan permitividad eléctrica y permeabilidad magnética, respectivamente, del medio en el que existen los campos eléctrico y magnético.
Estos dos parámetros e y m son, junto con s , los que tienen en cuenta las propiedades del medio material por el que la luz se propaga y en el caso de que dicho medio sea el espacio vacío se designan como e0 y m0 , que son dos constantes cuyos valores se han derivado de sucesivas mediciones y para los cuales se han llegado a establecer los siguientes (1) : e0 = 8.854 x 10 -12 F/m ,, m0 = 4p x 10 -7 H/m.
En el caso de que en el medio de propagación no exista una densidad neta de carga libre, es decir sea r = 0 , operando con las ecuaciones de Maxwell, llegamos a que :
 2 E - me 2 E - me  2E/ 2E/ t2 - ms t2 - ms  E/ E/ t = 0 t = 0
Esta ecuación es conocida como ecuación de ondas en el espacio libre de carga, en ella  2 representa el operador laplaciano, y de su solución obtenemos la forma matemática de los campos eléctrico y magnético de una onda electromagnética que se propaga en dicho espacio. 2 representa el operador laplaciano, y de su solución obtenemos la forma matemática de los campos eléctrico y magnético de una onda electromagnética que se propaga en dicho espacio.
Para obtener esta ecuación ya hemos impuesto la condición de que no haya carga eléctrica neta en el medio de propagación, si además imponemos la restricción de que no haya corrientes externas circulantes estaremos en una situación en la que quedan excluidas, del espacio de propagación que estamos considerando, las fuentes en las que el campo electromagnético se genera y las únicas corrientes que consideramos son las debidas a los fenómenos de conducción dieléctrica, las corrientes superficiales inducidas y otros fenómenos que dan lugar a una absorción en el medio y que se tienen en cuenta a través de la conductividad , s .
Por mayor sencillez consideraremos la propagación de la luz en regiones que están distantes del foco donde se origina, siendo las dimensiones de la sección del haz de radiación que consideramos muy pequeñas en relación con la distancia a la fuente o el origen de donde provienen.
En la práctica este es el caso cuando lo que observamos es un fenómeno que involucra la luz solar, dada la relación existente entre el tamaño de los objetos en los que observamos su interacción y la distancia desde éstos al Sol.
Algo equivalente sería considerar el haz de luz proviniente de una bombilla cuando sólo tomamos una pequeña parte del mismo que dejamos pasar a través de un orificio de dimensiones pequeñas comparadas con la distancia a la bombilla, esto es lo que se suele llamar un haz limitado.
Esto nos permitirá una mayor simplificación, al poder considerar que la propagación del campo se produce en una sola dirección, olvidándonos de las otras componentes angulares que en realidad existen pero que con las condiciones planteadas serán pequeñas y pueden no tenerse en cuenta.
Este tipo de ondas suelen llamarse ondas planas porque las amplitudes de los campos eléctrico y magnético son constantes en un plano perpendicular a la dirección de propagación de la onda y la ecuación de onda que habíamos planteado anteriormente y que tenía carácter tensorial debido al laplaciano, se reduce en este caso, suponiendo que la dirección de propagación es por ejemplo la del eje z, a la ecuación con carácter lineal siguiente:
 2E/ 2E/ z2 - me z2 - me  2E/ 2E/ t2 - ms t2 - ms  E/ E/ t = 0 t = 0
A partir de esta ecuación se obtiene la expresión de los vectores campo eléctrico y campo magnético como:
E = E0 e j(wt - gz) , , B = (g / w) uz x E
que son vectores oscilantes, siendo w la frecuencia angular de la oscilación, que es igual a 2pf donde f es la frecuencia temporal de la misma.
El vector uz es el vector unitario en la dirección de propagación, en este caso la dirección del eje z, y g es un parámetro cuya expresión en función de las otras variables se puede obtener sustituyendo la expresión de E en la ecuación de ondas y operando.
g = y + jh ,, siendo : y = ±w[em/2 ± (em/2)(1+(s/we)2)1/2]1/2 , , y h = - wms / 2y
El significado físico de el parámetro g lo podemos entender si consideramos el caso de una perturbación existente en un punto A , que puede describirse en función del tiempo por f(t) y que se propaga por el espacio con una velocidad v, hasta alcanzar un punto B que está separado del A por una distancia z.
 |
La perturbación que se observa en B en el instante de tiempo t será la misma que había en el punto A en el instante de tiempo (t-z/v), suponiendo que la perturbación no ha sufrido otras distorsiones y vendrá dada ahora por f(t-z/v).
En nuestro caso el campo eléctrico, para z=0, viene dado por E = E0 ejwt, y cuando se ha propagado una distancia z , por E = E0 ejw(t - (g/w)z), luego por analogía con el caso de la función f(t) ahora podríamos decir que (w/g) representa la velocidad con la que se propaga la perturbación del campo eléctrico.
Ahora bien, hemos visto que g es en términos generales un número complejo y por tanto la velocidad de propagación también debería serlo, lo cual no tiene mucho sentido y constituye una de las inconsistencias de la teoría electromagnética, que proviene del hecho de que para obtener la equivalencia de g con la velocidad de propagación hemos supuesto que la perturbación presente en el punto A se propaga hasta el punto B sin sufrir otro tipo de alteraciones o distorsiones y, en el caso de una onda electromagnética que se propaga en un medio con una conductividad eléctrica no nula, esto no se cumplirá porque existirá una cierta atenuación de la onda y también se producirá un cierto desfase entre los campos eléctrico y magnético de la misma.
En el caso de que la conductividad eléctrica , s, sea muy pequeña frente al producto we , se puede aproximar que y ~ w(em)1/2, y el campo eléctrico se puede expresar ahora como :
E = E0 ejw(t - (y /w)z) . e-wmsz/2y ~ E0 ejw(t - (em)1/2.z) . e-(m/e)1/2.s.z /2
En este caso, de medios dieléctricos con pequeña conductividad eléctrica y poco absorbentes de la radiación, se puede ver en la expresión del campo eléctrico que existe un factor de amortiguación que atenúa la señal con la distancia recorrida en el medio y que depende exponencialmente de la conductividad eléctrica, siendo la señal un campo oscilante de frecuencia angular w, que se propaga con una velocidad (em)-1/2.
Cuando la propagación es en el vacío, sustituyendo los valores de e0 y de m0 en la expresión de esta velocidad obtenemos como resultado el valor ; 2.99792 x 108 m/s que coincide con el valor determinado experimentalmente para la velocidad de la luz en el vacío y, considerando además que la conductividad eléctrica del vacío tiene un valor extremadamente pequeño, resulta que la señal se propaga por él sin sufrir prácticamente ninguna atenuación.
En el caso de ondas planas que estamos considerando, el vector amplitud máxima del campo eléctrico, E0e-jgz, sólo varía con la coordenada z y no con las coordenadas x e y, por lo que para que se cumpla la condición impuesta por la ley de Maxwell en el caso de que la densidad de carga libre sea 0, ley que se puede expresar como: div D = 0 , y si consideramos que el medio de propagación es homogéneo e isótropo, es decir e no depende de la posición, se tendrá que verificar que ;  Ez / Ez /  z = 0, y esto implicará que sea ; -jgEz = 0 lo cual sólo puede ser cierto si Ez = 0 o lo que es lo mismo que el vector campo eléctrico no tiene componente en la dirección z y se trata por lo tanto de un vector contenido en el plano de propagación, entendiendo por tal el plano en el que la amplitud del campo eléctrico es la misma para todos sus puntos y que es perpendicular a la dirección de propagación. z = 0, y esto implicará que sea ; -jgEz = 0 lo cual sólo puede ser cierto si Ez = 0 o lo que es lo mismo que el vector campo eléctrico no tiene componente en la dirección z y se trata por lo tanto de un vector contenido en el plano de propagación, entendiendo por tal el plano en el que la amplitud del campo eléctrico es la misma para todos sus puntos y que es perpendicular a la dirección de propagación.
De la expresión obtenida para el campo magnético, B, vemos que también es un vector perpedicular a la dirección de propagación y al campo eléctrico, al ser proporcional al producto vectorial de éste y el vector unitario en la dirección de propagación, por lo cual también estará contenido en el que hemos llamado plano de propagación y estará en fase de oscilación con el campo eléctrico cuando g tenga un valor real, es decir cuando sea s = 0, existiendo un cierto desfase en otro caso.
 |
Una representación muy utilizada para los campos eléctrico y magnético de una onda electromagnética plana que se propaga a lo largo de la dirección z, se puede ver en la figura en la que se presenta una instantánea tridimensional de dichos campos en la cual los mismos se visualizan como vectores cuya longitud, dirección y sentido representan la intensidad del campo, su dirección y su sentido, respectivamente.
Ésta es sólo una posible representación de los campos, quizá no la más adecuada, puesto que en realidad lo que deberíamos representar son intensidades de campo y no longitudes y ello podría hacerse representando densidades de líneas de fuerza por unidad de longitud o algo similar, pero una tal representación necesitaría también por nuestra parte de un cierto grado de abstracción, por lo que podemos hacer dicha abstracción sobre el dibujo de la figura, que es de visualización más sencilla.
En ella podemos ver que la longitud de onda, que suele designarse con la letra l , es la distancia a lo largo de la cual se completa un ciclo entero de oscilación, es decir será la distancia z, recorrida en el tiempo t, dividida por el número de ciclos que se han producido en ese tiempo o, dicho de otra forma, será la velocidad de propagación dividida por la frecuencia:
l = v/f , que también se puede poner como : l = v.T , siendo T = 1/f , el periodo de la oscilación.
También podemos poner, puesto que hemos visto anteriormente que es v = w/g, que otra expresión para la longitud de onda es : l = 2p/g , o bien que : g = 2p/l, donde una vez más hay que decir que el concepto de longitud de onda tiene pleno sentido en el caso de medios de propagación no absorbentes en los que tiene un valor real, siendo en otro caso una magnitud compleja de difícil interpretación.
En cuanto a la energía transportada por la onda lo será por los campos eléctrico y magnético de la misma y dependerá de la energía suministrada a la fuente en la que el campo electromagnético se genera, debiendo mantenerse el equilibrio energético entre energía aportada a dicha fuente, energía almacenada en la misma y energía radiada o perdida en forma de campos que se propagan alejándose de la fuente.
En esta ecuación de balance energético la energía transportada por el campo electromagnético suele expresarse en función del llamado vector de Poynting, que se define como: P = E x H , y de su flujo a través de una superficie cerrada que encierre el volumen donde se encuentran las fuentes, siendo dicho flujo igual a la velocidad de paso de la energía por dicha superficie, lo que se conoce como flujo de energía.
En este momento es conveniente detenerse un poco a considerar qué tipo de campo estamos manejando, es decir ¿qué representan estas ondas planas y homogéneas cuyas expresiones matemáticas hemos obtenido?
Podríamos plantearnos, tal y como se hace en algunos textos (2), si sería posible identificar una onda de esas características y en ese caso tendríamos que estar de acuerdo en que la respuesta es negativa, puesto que la onda de la que estamos hablando es tal que no se le han impuesto restricciones en cuanto a su existencia temporal se refiere, es decir habría existido siempre y por siempre existiría, y sabemos que para poder detectar un fenómeno cualquiera necesitamos que se produzca alguna variación en él.
En efecto, cualquier campo o señal real tiene un comienzo y un final y ello supone también que no se podrá describir por una oscilación de una sola frecuencia, sino por una superposición de multitud de oscilaciones de diferentes frecuencias que cubrirán un cierto intervalo o anchura espectral [-Dw , Dw].
Existen casos, como en la radiación emitida por los láseres, en que este intervalo es muy estrecho y se dice que la radiación por ellos emitida es casi monocromática, pero siempre involucra un intervalo finito de frecuencias y hay otros casos en los que la radiación comprende una banda muy amplia y contínua de frecuencias, como es el de la radiación proviniente del Sol y de otras fuentes de radiación como los cuerpos incandescentes, las llamas del fuego y otros muchos.
A pesar de esta limitación, el concepto de onda plana homogénea resulta de gran utilidad en tanto que simplifica mucho el tratamiento matemático de los fenómenos que nos proponemos abordar, evitando que continuamente tengamos que considerar adiciones e interferencias de las componentes espectrales de las señales que se propagan, y podamos limitar el problema a ondas monocromáticas que nos permitirán obtener expresiones válidas para multitud de situaciones reales en las que los espectros de energía de la radiación considerada se pueden aproximar por una suma de cierto número de bandas de energía de radiaciones casi monocromáticas.
Además, las ecuaciones planteadas y las expresiones obtenidas para los campos tienen validez para todo el rango de frecuencias del espectro electromagnético, que abarca desde frecuencias muy bajas, de campos casi estáticos, hasta las frecuencias más altas conocidas, de los rayos cósmicos, pasando por todas las correspondientes a frecuencias de radio, radiaciones infrarrojas, visibles, ultravioletas, y rayos-x como puede verse en la figura.

Imagen reproducida de : http://www.sapiensman.com/ESDictionary/E/Technical_vocabulary_Spanish(E6).htm
|
En cuanto a los medios por los que la radiación se propaga ya hemos visto que se pueden caracterizar por la permitividad eléctrica , e , la permeabilidad magnética , m y la conductividad eléctrica , s , parámetros que determinan la propagación del campo en dichos medios materiales.
Un medio material está compuesto por átomos, que a su vez pueden organizarse formando moléculas y éstas pueden presentar momentos dipolares eléctricos, ya sean permanentes o sean inducidos por los campos eléctricos externos, y momentos magnéticos a nivel atómico y molecular, que interaccionarán con los campos eléctrico y magnético, respectivamente, de la radiación electromagnética.
En el caso de campos cuya frecuencia de oscilación es baja, las moléculas y los átomos oscilarán siguiendo la frecuencia del campo por lo que e y m serán magnitudes reales que relacionan los campos de polarización y magnetización inducidos en el material con los campos externos de la onda, pero en el caso de campos electromagnéticos de alta frecuencia, como ocurre con las radiaciones ópticas, los átomos y moléculas no pueden seguir a los campos en su oscilación, produciéndose desfases entre los campos actuantes y los campos inducidos, lo que hace que e y m tengan ahora carácter vectorial o complejo, por lo que supondremos de una forma genérica que siempre se pueden describir por magnitudes complejas.
También se pueden expresar e y m en relación a las constantes de permitividad y permeabilidad del vacío , e0 y m0 , como ; e = ke.e0 , , m = km.m0 , donde ke y km reciben el nombre de constante dieléctrica y permeabilidad relativa del material, respectivamente (3).
Estos parámetros se suelen utilizar de forma alternativa a la permitividad y permeabilidad para caracterizar los medios materiales dado que e0 y m0 son invariables.
También la velocidad de propagación de la onda, que en el caso de medios poco absorbentes se podía expresar como ; v = 1/(e . m)1/2 , ahora se podrá expresar de la siguiente forma ; v = [1/(e0 . m0)1/2].[1/(ke.km)1/2] y como el término del primer corchete es la velocidad de propagación de la luz en el vacío , c , podremos poner que la velocidad de propagación en un medio de constantes ke y km , es ; v = c /(ke.km)1/2.
La magnitud (ke.km)1/2 se denomina índice de refracción del medio, se suele designar como N y expresa la relación que existe entre la velocidad de la onda en el vacío y en el medio caracterizado por dicho índice de refracción.
El valor de la constante km es aproximadamente igual a 1 para casi todos los materiales, con excepción de los ferromagnéticos, por lo que en la mayoría de los casos será ; N = (ke)1/2 , y el material se puede caracterizar por su constante dieléctrica o alternativamente por la raiz de ésta, es decir por su índice de refracción N , que será en general un número complejo que suele designarse por : N = n - jk , donde n es conocido como índice real de refracción y k la constante de amortiguamiento que a veces también se relaciona con el llamado coeficiente de extinción , c , por medio de ; k = n . c
Tradicionalmente se ha caracterizado el comportamiento de los medios materiales, frente a los campos electromagnéticos, por la constante dieléctrica para los campos de frecuencias bajas y medias, y por el índice de refracción para los campos de frecuencias muy altas, las llamadas frecuencias ópticas.
Es por ello que los datos obtenidos en las medidas experimentales realizadas, se encuentran recogidos en tablas de constantes dieléctricas y de índices de refracción según que la medida se haya hecho con campos de frecuencias bajas o de frecuencias ópticas, respectivamente.
Tanto la constante dieléctrica como el índice de refracción son magnitudes cuyo valor es mayor que la unidad, cubren un rango de valores entre 1 y 100 aproximadamente, y presentan una dependencia con la temperatura a la que se encuentra el material, disminuyendo al aumentar ésta en la mayoría de los casos, lo cual está de acuerdo con la interpretación que se hace de la permitividad, ya que una mayor temperatura supone mayor nivel de agitación de los átomos y moléculas del material y mayor dificultad para orientar los momentos eléctricos y magnéticos por acción del campo.
Al representar el índice de refracción por un número complejo se pueden tener en cuenta, en la representación matemática de la transmisión y reflexión de la radiación, los procesos de absorción que tienen lugar en los medios materiales y se puede cuantificar dicha absorción de una forma genérica, independientemente del proceso físico concreto que la produce.
Estos procesos que dan lugar a la absorción de radiación electromagnética en el interior de los medios materiales son de diversos tipos y dependen del tipo de material y de radiación que interaccionan, siendo los componentes elementales de la materia, electrones, átomos y moléculas, los que dan lugar a dicha absorción, dependiendo de sus masas, su configuración electrónica y sus energías de enlace, respectivamente.
Así por ejemplo, los electrones libres en la banda de conducción de metales y semiconductores, con su pequeña masa, pueden oscilar a muy altas frecuencias y son los responsables de la absorción de radiación en prácticamente todo el espectro electromagnético.
Los electrones ligados, situados en las capas internas de la configuración electrónica de los átomos de materiales semiconductores y dieléctricos, requieren de mayores energías para romper las ligaduras y pasar a niveles superiores de energía dentro de dicha configuración y por ello absorben radiación en las bandas del visible, ultravioleta, rayos-X y frecuencias superiores.
Los átomos, como conjunto, pueden oscilar bajo la influencia del campo electromagnético, en especial cuando presentan momentos dipolares eléctricos, sean éstos permanentes o inducidos por el campo, y teniendo en cuenta su mayor masa es lógico que dicha oscilación se produzca cuando interaccionan con radiaciones de menor frecuencia, generalmente en el rango del infrarrojo y de las microondas.
Los distintos tipos de oscilaciones posibles de los átomos dentro de una molécula dada dependerán de su configuración y del tipo de enlaces presentes, pudiendo requerir mayor o menor energía para producirse y por tanto dando lugar a la absorción de radiaciones de distintas frecuencias, según que dichos movimientos involucren el estiramiento de enlaces, la vibración o la torsión de los mismos.
Por otra parte hemos visto que, en medios no absorbentes, el índice de refracción indica la relación existente entre la velocidad con que se propaga la radiación en el vacío y en el medio material considerado, velocidad que será tanto menor cuanto mayor sea dicho índice de refracción.
Así por ejemplo en el aire, cuyo índice de refracción para frecuencias en el rango de la radiación visible es de 1.0003 aproximadamente, la velocidad de propagación de la luz es un 33% mayor que en el agua cuyo índice de refracción es de 1.333 aproximadamente, lo cual produce, entre otros fenómenos, que nuestro sentido de la vista, acostumbrado a estimar las distancias entre objetos en el aire, interprete que los objetos sumergidos en el agua se encuentran más próximos de nosotros de lo que realmente están.
En este efecto tiene también influencia la presencia de la interfase que separa los dos medios, una superficie plana en muchos casos, y los procesos que tienen lugar cuando la radiación atraviesa dicha superficie.

INTERACCIÓN CON SUPERFICIES
Una onda plana monocromática que se propaga en una cierta dirección, dentro de un medio homogéneo caracterizado por una permitividad eléctrica e1 y por una permeabilidad magnética m1 , seguirá indefinidamente propagándose en esa dirección si no encuentra en su camino algo que altere su trayectoria, algo como un campo de energía o la presencia de otro medio material con propiedades distintas a aquel del que proviene.
Sabemos que una tal onda, que se propaga en la dirección del eje z, puede estar caracterizada por un campo eléctrico y un campo magnético cuyas expresiones son:
E = E0 e j(wt - g1z) , , B = (g1 / w) uz x E
Si esta onda encuentra en su camino otro medio material de permitividad e2 y permeabilidad m2, la separación entre ambos medios se podrá describir habitualmente por una superficie S de cuyas características dependerá la forma en que se produce la transición entre los campos existentes en el primer medio, llamado medio de incidencia, y el segundo medio, llamado medio de emergencia.
Esta superficie se puede aproximar en muchos casos por un plano y la situación se puede representar como la mostrada en la figura, en la que el campo electromagnético incide sobre la superficie formando un ángulo a con la normal a la misma y resulta parcialmente reflejado hacia el medio de incidencia y parcialmente transmitido dentro del segundo medio con direcciones y amplitudes que vendrán fijadas por las condiciones de continuidad que han de cumplir los campos al atravesar la superficie.
 |
El plano en el que están contenidas las direcciones de incidencia, reflexión y transmisión, en la figura el plano XZ, se suele llamar plano de incidencia y puede demostrarse que siempre es perpendicular a la superficie plana del medio sobre la que incide la radiación.
En un caso como el representado en la figura, en el que la onda incidente se propaga en una cierta dirección que forma un ángulo a con el eje z, el exponente en la expresión del campo contendrá, en vez de g1z, una expresión de la forma ; g1(x.sen a + z.cos a), e igual sucedería con la onda reflejada en el medio 1, excepto que en este caso el ángulo sería el ángulo adyacente al a.
En el caso de la onda transmitida, el exponente de los campos tendrá también una expresión que será de la forma ; g2(x.sen b + z.cos b) , siendo b el ángulo que forma la dirección de propagación de la onda transmitida con el eje z.
La condición de continuidad de las componentes tangenciales de los campos en la frontera entre los dos medios, exige (4) que los exponentes en las expresiones de los campos sean iguales para z=0 .
Es decir que deberá cumplirse que:
g1.sen a = g1.sen a = g2.sen b
La primera igualdad es realmente una identidad, pues ya habíamos supuesto que el ángulo de reflexión es igual al ángulo de incidencia, a , y esta observación recibe el nombre de primera ley de Snell, cuya aplicación es muy frecuente cuando se trabaja con espejos o superficies esencialmente reflectantes.
De la otra igualdad deducimos que ; sen b / sen a = g1 / g2 , que se puede expresar también, recordando que g = w / v , y que v = c / N , como :
sen b / sen a = N1 / N2 ,, o bien que: N1.sen a = N2.sen b
Esta ecuación expresa la relación entre el ángulo de incidencia y el de refracción en función de los índices de refracción de ambos medios, recibe el nombre de segunda ley de Snell, y permite predecir cual será el ángulo con que emerge un rayo de luz que incide con un cierto ángulo sobre la superficie plana de separación entre dos medios materiales de índice de refracción conocido.
Esta ley nos permite comprender, por ejemplo, el conocido efecto que se observa al introducir un palo recto o varilla en el agua, en el cual se percibe la parte sumergida de dicho objeto como si estuviera torcida un cierto ángulo con respecto a la parte que se encuentra en el exterior y también explica por qué necesitamos gafas de bucear para poder ver mejor debajo del agua, ya que nuestros ojos están adaptados a ver en el aire produciendo la refracción de los rayos luminosos y la correcta formación de las imágenes cuando la relación entre los índices de refracción del medio de incidencia y el de emergencia es precisamente la que corresponde al aire y al humor acuoso de la córnea del ojo, respectivamente. Si en vez del aire el medio de incidencia es el agua, el ojo no es capaz de adaptarse para producir la refracción dada la nueva relación que ahora existe entre los índices de refracción de los dos medios en contacto y ello se supera utilizando las gafas de bucear que siguen manteniendo el aire como medio de incidencia en contacto con el ojo.
También se hace uso de esta ley en aplicaciones tan importantes de la industria óptica como son el diseño y la fabricación de lentes, lupas, objetivos de microscopio, prismas y otros muchos dispositivos.
Aquí hay que decir que, tal y como ya hemos visto antes, g1 y g2 son números complejos cuando las conductividades de los dos medios no son nulas y, por tanto, como el ángulo de incidencia es un número real, el sen b será en general también complejo lo cual significa que en este caso habrá absorción en el segundo medio a lo largo de la dirección z , los planos de propagación de fase constante y de amplitud constante ahora no coinciden y se dice que la onda en el segundo medio, aunque sigue siendo plana, ya no es homogénea.
En este caso el ángulo que forma la normal al frente de onda con el eje z se indica por medio de un ángulo j , que se llama ángulo de refracción verdadero, que es real y que operando se obtiene como :
tg j = g1.sen a / Re [g22 - g12.sen2 a]1/2
Donde Re significa "parte real de" y se puede demostrar que cuando el segundo medio es débilmente absorbente y su índice de refracción algo mayor que el del medio de incidencia, se cumple que tg j es aproximadamente igual al módulo de tg b.
Si por el contrario el medio de emergencia es muy absorbente o su índice de refracción es mucho mayor que el de el medio de incidencia, entonces el ángulo j tiende a cero y la onda se propaga en el segundo medio en una dirección muy próxima a la del eje z.
La segunda ley de Snell es también útil para la explicación del fenómeno de la reflexión total, que sucede cuando el índice de refracción del medio de incidencia , N1 , es mayor que el del medio de emergencia , N2 , y la incidencia se produce bajo un ángulo igual o mayor que el determinado por la relación : sen a = (N2 / N1) , ángulo que se conoce con el nombre de ángulo límite o crítico, para el cual se debe verificar que sen b es igual a 1 para cumplir la segunda ley de Snell y por lo tanto b debe ser 90º, por lo que para dicho ángulo de incidencia existirá una onda que se propaga en dirección paralela a la superficie plana de separación de los medios y para ángulos mayores no existirá radiación transmitida y toda será reflejada.
Este efecto se puede observar en el caso de el fenómeno conocido como espejismo, que suele producirse cuando se miran desde lejos superficies muy calientes, como es el caso de la arena del desierto y también el de las carreteras o pistas de asfalto expuestas al sol, en las que la superficie aparenta ser un medio muy reflectante, como el agua, debido a que se forma una lámina de aire muy caliente en contacto con la superficie, aire cuyo índice de refracción es menor que el del aire frio adyacente desde el que incide la luz, que se refleja totalmente cuando se observa desde ángulos superiores al crítico o límite.
El efecto de la reflexión total se utiliza también, entre otras aplicaciones, en la transmisión de señales luminosas a través de fibras ópticas con una mínima pérdida de la intensidad de la señal, gracias a que ésta queda confinada al interior de la fibra óptica por el efecto de la reflexión total.
Para comprender mejor la interacción del campo con la superficie sería necesario, además de conocer la dirección en que se propagan las ondas reflejada y transmitida, saber cual es la intensidad de los campos asociados a cada una de ellas y las características de los mismos.
Para ello seguimos manteniendo la hipótesis de que la superficie de separación es plana y en el caso de que la onda incidente forme un ángulo cualquiera , a , con la dirección del eje z , tenemos que considerar también cuál es la orientación de los campos con respecto al plano de incidencia, orientación que es lo que se suele llamar la polarización de la onda.
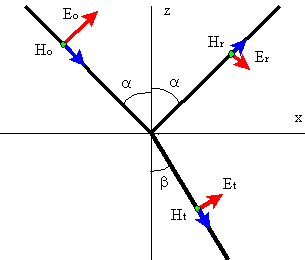
Para una polarización cualquiera, los vectores de los campos eléctrico y magnético, que son perpendiculares entre sí y a la dirección de propagación, podrán formar un ángulo cualquiera con el plano de incidencia pero siempre se podrán expresar como la suma o combinación de dos tipos de orientación o polarización, una en la que el vector campo eléctrico es perpendicular al plano de incidencia, caso representado en la anterior figura, que se llama polarización perpendicular, y otra en la que el vector campo eléctrico está contenido en el plano de incidencia, que se conoce como polarización paralela y que se representa de forma bidimensional en la figura siguiente, en la que el campo magnético se visualiza con un punto verde indicando que es perpendicular al plano de la figura, saliendo hacia fuera de la misma.
Por tanto será suficiente con resolver estos dos casos por separado para después poder expresar cualquier otro como una combinación de ellos.
 |
En el caso de la polarización con el campo eléctrico perpendicular al plano de incidencia, las expresiones de los campos de la onda incidente se pueden poner como:
E0 = uy E0i ejwt e-jg1(x sen a + z cos a)
H0 = E0i (g1/m1 w ) (ux cos a - uz sen a) ejwt e-jg1(x sen a + z cos a)
en donde ux , uy , uz son los vectores unitarios en la dirección de los ejes x , y , z , respectivamente.
Para los campos de la onda transmitida tendremos :
Et = uy E0t ejwt e-jg2(x sen b + z cos b)
Ht = E0t (g2/m2 w ) (ux cos b - uz sen b) ejwt e-jg2(x sen b + z cos b)
en donde ux , uy , uz tienen el mismo significado que antes y b es el ángulo de refracción que forma el rayo transmitido con el eje z.
Por último, para los campos de la onda reflejada, en el caso de la polarización perpendicular, tendremos :
Er = uy E0r ejwt e-jg1(x sen a - z cos a)
Hr = -E0r (g1/m1 w ) (ux cos a + uz sen a) ejwt e-jg1(x sen a - z cos a)
Se pueden ahora introducir los que se conocen como coeficiente de reflexión , r , y coeficiente de transmisión , t , de la superficie para la onda con polarización perpendicular, que se definen como :
rs = E0r / E0i , , ts = E0t / E0i
Aplicando las condiciones de continuidad de las componentes tangenciales en la frontera entre los dos medios, llegamos a que :
E0i + E0r = E0t , y a que : (g1/m1 w ).(E0i - E0r).cos a = (g2/m2 w ).E0t.cos b
Ahora operando con estas expresiones podemos poner los coeficientes de reflexión y transmisión de los campos en la superficie de separación de los medios, para el caso de polarización perpendicular, como :
rs = [(g2/m2 w ) cos a - (g1/m1 w ) cos b] / [(g2/m2 w ) cos a + (g1/m1 w ) cos b]
ts = 2 (g1/m1 w ) cos a / [(g2/m2 w ) cos a + (g1/m1 w ) cos b]
expresiones que se conocen con el nombre de fórmulas de Fresnel.
En el caso de la polarización con el campo eléctrico contenido en el plano de incidencia, conocida como polarización paralela, las expresiones de los campos de la onda incidente se pueden poner como:
E0 = E0i (ux cos a - uz sen a) ejwt e-jg1(x sen a + z cos a)
H0 = -uy E0i (g1/m1 w ) ejwt e-jg1(x sen a + z cos a)
Análogamente tendremos para la onda transmitida :
Et = E0t (ux cos b - uz sen b) ejwt e-jg2(x sen b + z cos b)
Ht = -uy E0t (g2/m2 w ) ejwt e-jg2(x sen b + z cos b)
y para la reflejada :
Er = -E0r (ux cos a + uz sen a) ejwt e-jg1(x sen a - z cos a)
Hr = -uy E0r (g1/m1 w ) ejwt e-jg1(x sen a - z cos a)
Si se igualan las componentes tangenciales de los campos en la interfase, igual que se hizo en el caso de la polarización perpendicular, se pueden obtener ahora los factores de reflexión y transmisión para el caso de la polarización paralela, las llamadas fórmulas de Fresnel para polarización paralela, que se pueden expresar como:
rp = [(g2/m2 w ) cos b - (g1/m1 w ) cos a] / [(g2/m2 w ) cos b + (g1/m1 w ) cos a]
tp = 2 (g1/m1 w ) cos a / [(g2/m2 w ) cos b + (g1/m1 w ) cos a]
A partir de las expresiones de los coeficientes de reflexión de la superficie para las ondas polarizadas, perpendicular y paralela, podemos extraer una consecuencia interesante si nos planteamos la posibilidad de que dicho coeficiente de reflexión se anule completamente para algún ángulo de incidencia concreto, dependiendo de las propiedades de los medios de incidencia y emergencia.
Para ello, considerando por simplificar el caso en que no hay absorción y sustituyendo el cos b en las expresiones de los coeficientes de reflexión por medio de la segunda ley de Snell, expresándolo en función de a e igualando a cero los numeradores de dichos coeficientes, obtenemos la siguiente condición para el caso de la polarización perpendicular.
sen2 a = [(e2 / e1) - (m2 / m1)] / [(m1 / m2) - (m2 / m1)]
Operando análogamente para la polarización paralela obtenemos la condición:
sen2 a = [(m2 / m1) - (e2 / e1)] / [(e1 / e2) - (e2 / e1)]
En estas expresiones vemos que no siempre es posible que exista algún ángulo de incidencia que cumpla dichas condiciones, en particular en el caso de la polarización perpendicular no será posible para la mayor parte de los materiales dieléctricos no magnéticos, para los que es : m1 = m2 = m0.
No ocurre lo mismo para la polarización paralela para la que obtenemos, sustituyendo m1 = m2 = m0 en la expresión correspondiente de sen2 a , la siguiente condición para el ángulo de incidencia :
a = arctg (e2 / e1)1/2 = arctg (N2/N1)
ángulo para el que no habrá campo reflejado y que se conoce como ángulo de Brewster.
El hecho de que para ese mismo ángulo el coeficiente de reflexión para la onda con polarización perpendicular no sea nulo, implica que toda la radiación que se refleje bajo dicho ángulo de incidencia en esa superficie tendrá polarización perpendicular independientemente de la polarización de la onda incidente y esto proporciona un método para obtener radiación polarizada con una orientación fija para diferentes aplicaciones en las que se necesite tal polarización.
Los coeficientes de reflexión y transmisión que se han obtenido relacionan las amplitudes de los campos reflejado y transmitido con la del incidente, pero en la mayoría de las situaciones prácticas lo que podremos observar o medir será la energía transportada por dichos campos y por ello es conveniente definir otras magnitudes que relacionen la energia de los campos reflejado y transmitido con la energía del campo incidente y obtener sus expresiones.
Estas magnitudes son las que se conocen como reflectancia y transmitancia de la superficie y se definen en función de los vectores de poynting de los campos reflejado, transmitido e incidente como ;
_________ __________
R = Re [Er x Hr] / Re [E0 x H0]
_________ __________
T = Re [Et x Ht] / Re [E0 x H0]
expresiones que representan, respectivamente, los promedios temporales de la densidad del flujo de energía reflejada y transmitida respecto de la incidente.
De su cálculo para el caso sencillo de incidencia normal, en cuyo caso el estado de polarización de la onda no influye en las expresiones de los coeficientes de reflexión y transmisión , incidencia que se produzca sobre una superficie de separación entre dos medios materiales no absorbentes, de índices de refracción reales, N1 y N2 , para la que dichos coeficientes de reflexión y de transmisión de los campos se pueden simplificar a : r = (N1 - N2) / (N1 + N2) , t = 2 N1 /(N1 + N2) , y aplicando las definiciones anteriores resultan las siguientes expresiones para la reflectancia y la transmitancia ;
R = [(N1 - N2) / (N1 + N2)]2 , , T = (N2/N1)[2 N1 /(N1 + N2)]2
que, por ejemplo, para el caso frecuente de una superficie de vidrio ( N2=1.5 ) en el aire ( N1=1 ) dan como resultado los valores R = 0.04 y T = 0.96 por lo que vemos que en este caso de una sola superficie, la energía se refleja o se transmite pero no se absorbe ni se almacena en la interfase de los medios.
Esto sucede cuando hemos considerado que tanto el medio de incidencia como el medio de emergencia son semi-infinitos lo cual no suele ocurrir en la realidad porque, si bien en el caso de que el medio de incidencia sea el aire es razonable considerar el medio de incidencia como semi-infinito, en el caso del medio de emergencia lo habitual es que sea un medio material limitado en algún momento por al menos una segunda superficie que también tendrá influencia sobre los valores de los coeficientes obtenidos.
Una excepción sería el caso en que el medio de emergencia fuese por ejemplo el agua del mar la cual, dada su gran profundidad, se podría también considerar como un medio semi-infinito.
En el caso de que el segundo medio esté limitado por una segunda superficie, dicha superficie reflejará y transmitirá a su vez la radiación transmitida por la primera y así dará lugar a una radiación reflejada adicional, disminuyendo la radiación que se transmitiría a un tercer medio posterior que sería ahora el medio de emergencia.
Si por simplificar suponemos que dicha segunda superficie es también plana y paralela a la primera, una posible aproximación a la solución del problema fué primero sugerida por Airy en 1833 (5) y consiste en suponer que el proceso se produce secuencialmente, es decir que de la radiación incidente sobre la primera superficie una parte se refleja en ella y otra se transmite hacia la segunda superficie del segundo medio, recorriendo una cierta distancia en la que sufre un cierto desfase, allí nuevamente una parte de ella se transmite al tercer medio y otra se refleja hacia la primera superficie, sufriendo el correspondiente desfase adicional, donde a su vez vuelve a ocurrir el mismo proceso y así sucesivamente tal y como se representa en la figura siguiente.

En ella se verifica además que r´e = - re y el desfase sufrido por el haz en cada paso por el espesor, d , de la lámina se puede demostrar (6) que viene dado por : d = g2.d.cos b , siendo b el ángulo bajo el que se refracta el haz de radiación incidente en el segundo medio.
Si sumamos todas las contribuciones a los campos reflejado y transmitido, respectivamente, sin tener en cuenta la dependencia del tiempo que es la misma para todas, obtenemos unas sumas de series con expresiones del tipo:
Er . ejy = E0 . [re+ te t´e re1 . e-2jd . ( 1 + re1. r´e . e-2jd + re12 r´e2 . e-4jd + ....)]
Et . ejz = E0 . te te1 . e-jd . ( 1 + re1. r´e . e-2jd + re12 r´e2 . e-4jd + ....)
En estas expresiones la serie que aparece entre paréntesis es una serie geométrica covergente, por lo que calculando el valor de su suma y teniendo también en cuenta que tet´e - rer´e = 1 , lo cual se puede comprobar fácilmente, llegamos a que las resultantes de los campos reflejado y transmitido se pueden expresar como:
Er . ejy = E0 . [(re + re1 . e -2jd)/(1 + re . re1 . e -2jd)]
Et . ejz = E0 . te . te1 . e-jd /(1 + re . re1 . e -2jd)
De las definiciones de reflectancia y transmitancia que también pueden expresarse como;
R = |Er|2 / |E0|2 , , , T = Re(g2/g1) .|Et|2 / |E0|2
vemos que las expresiones de la reflectancia y transmitancia para el caso planteado de la lámina con superficies plano-paralelas , se podrían calcular multiplicando Er . ejy / E0 por su complejo conjugado y multiplicando Et . ejz / E0 por Re(g2/g1) y por su complejo conjugado, respectivamente.
Estos cálculos no son difíciles, aunque sí algo laboriosos y se simplifican bastante para el caso de incidencia normal, para cuyo caso se pueden encontrar las expresiones algebraicas resultantes de este calculo en (7).
Son muchos los ejemplos cotidianos en los que podemos encontrar un sistema de este tipo, formado por un material limitado por dos superficies planas y paralelas, como es el caso del vidrio de una ventana, la lente de una gafa, una lámina de plástico transparente, el ala de un insecto o la hoja translúcida de un vegetal.
Las expresiones anteriores han sido deducidas para el caso ideal de una onda plana monocromática de longitud de onda l, lo cual no corresponderá con las situaciones que encontremos en la realidad en las que la radiación tendrá longitudes de onda comprendidas en un cierto intervalo [l-Dl/2 , l+Dl/2], siendo Dl lo que se conoce como ancho de banda del haz de radiación.
En este caso de un ancho de banda finito, podemos hacer una extensión de las expresiones deducidas, teniendo en cuenta el principio de superposición de los campos electromagnéticos, sumando todas las contribuciones a los campos reflejado y transmitido procedentes de todas las componentes espectrales dentro del intervalo de longitudes de onda de la radiación incidente, lo cual se conseguiría integrando las expresiones de dichos campos entre los límites del intervalo [d-Dd/2 , d+Dd/2] multiplicadas por la función que defina la distribución espectral de la radiación incidente dentro de dicho intervalo.
Estos cálculos suelen realizarse de forma numérica, utilizando ordenadores o máquinas de cálculo automático, pero hay casos en los que se pueden simplificar mucho y en los que pueden llegar a realizarse de forma muy sencilla, en especial cuando se cumplen ciertas condiciones con respecto al material de la lámina y con respecto al ángulo de incidencia y al ancho de banda de la radiación incidente.
Con respecto a las propiedades de la lámina se puede decir que los materiales con pequeña absorción se pueden caracterizar de forma aproximada por un índice de refracción real, N , y con respecto a la radiación, en el caso de que la incidencia sea normal las expresiones se simplifican notablemente ya que no dependen de la polarización de la onda incidente, y si adicionalmente el ancho de banda es suficientemente grande esto hace que las expresiones puedan simplificarse aún más.
Cuando se trabaja con radiación electromagnética de frecuencias ópticas el parámetro que suele utilizarse para su caracterización espectral es la longitud de onda (8) , por ello veamos cual es la equivalencia entre el ancho de banda espectral expresado en longitud de onda , Dl , y el ancho de banda expresado por el desfase , Dd .
Se ha visto antes que el desfase sufrido por la radiación dentro de la lámina viene dado por ; d = g2.d.cos b , siendo g2 = 2.p.N2 / l , donde l es la longitud de onda de la radiación en el vacío y N2 el índice de refracción del material de la lámina, por lo que d se podrá expresar como : d = 2.p.N2.d.cos b / l
A partir de aquí, suponiendo que N2 no depende de l , tendremos ;
|Dd| = (2.p.N2.d.cos b).|Dl| / l2 => |Dd| = (2.p.N2.d.cos b) / (l2 / |Dl|)
expresión en la que reconocemos la presencia de la que es conocida (9) como longitud de coherencia de la radiación , l2 / Dl .
En el caso de incidencia normal será b = 0 y las sucesivas contribuciones a la onda transmitida darán lugar a máximos de interferencia cuando el desfase sufrido al atravesar la lámina sea igual a p radianes o un múltiplo entero de p , ya que al atravesar la lámina dos veces o un múltiplo entero de dos la onda que emerja, proviniente de las reflexiones internas en la lámina, volverá a estar en fase con la transmitida dando lugar a la interferencia constructiva.
Así, cuando por ejemplo se realiza la medida de el espectro de transmisión de una lámina, registrando el valor de la transmitancia frente a la longitud de onda, al variar la longitud de onda varía el desfase y pasaremos de un máximo de interferencia al siguiente cuando esta variación corresponda a una magnitud de p radianes en el desfase, recorriendo todos los valores intermedios y pasando por un mínimo de interferencia que corresponderá a un incremento en el desfase de p/2, en el cual la interferencia es destructiva.
Entonces, para incidencia normal y considerando que la radiación es monocromática, las condiciones que cumplirán los máximos y los mínimos de transmitancia serán respectivamente :
2.Nmax.d = m.lmax , para los máximos y ; 4.Nmin.d = (2 m + 1).lmin , para los mínimos.
donde Nmax y Nmin representan los valores que toma el índice de refracción para las longitudes de onda lmax y lmin a las que se producen el máximo y el mínimo de interferencia, respectivamente, siendo m un número entero que se conoce como orden de interferencia, que indica el número de veces que p esta contenido en el desfase que se produce en la radiación al atravesar la lámina.
Se pueden presentar dos situaciones límites en la relación entre el espesor óptico de la lámina , N2.d.cos b , y la longitud de coherencia de la radiación , l2 / Dl , una en la que el espesor óptico de la lámina es mucho menor que la longitud de coherencia del haz, que corresponderá entonces a valores de Dd mucho menores que 2p , lo cual supondrá integrar las expresiones de los coeficientes de reflexión y transmisión sobre un intervalo muy pequeño y produciría resultados parecidos a considerar la radiación como monocromática, y otra en la que el espesor óptico de la lámina es mucho mayor que la longitud de coherencia de la radiación, que llevaría a valores de Dd mucho mayores que 2p lo que supondría integrar los coeficientes sobre intervalos grandes y llevaría a la desaparición de las diferencias de visibilidad entre máximos y mínimos de interferencia, llegándose a valores medios independientes del valor del desfase y del espesor óptico de la lámina.
En este segundo caso se pueden calcular la reflectancia y transmitancia del sistema por un método similar al de Airy, pero utilizando las transmitancias y reflectancias de cada superficie y sin considerar los efectos del desfase, que para el caso considerado de una lámina no absorbente inmersa en un medio semiinfinito se podrán calcular como :
R = R1 + T1 T2 R2 /(1- R22) T = T1 T2 /(1- R22)
en donde T1 , R1 , T2 y R2 , son las transmitancias y reflectancias de la primera y segunda superficie, respectivamente, que se pueden calcular en función de los índices de refracción de los dos medios tal y como hemos visto antes y que calculando para el caso de una lámina de vidrio con N2=1.5 en el aire, rinden los valores ; T = .923 , R = .077 .
Estos valores indican que, si por ejemplo la lámina de vidrio es la de una ventana, el 92.3% de la luz que incide sobre la ventana la atraviesa y el 7.7% resulta reflejada, no absorbiéndose ninguna radiación en el material, lo cual será bastante bien aproximado a la realidad sólo para algunos tipos de radiación como la luz visible, pero no será cierto para otros, como es el caso de las radiaciones en el rango del ultravioleta y del infrarrojo medio en las que el vidrio de la ventana absorbe la radiación y por lo tanto no sería correcto considerar el índice de refracción del vidrio como un número real en estos rangos de longitudes de onda.
En realidad, en esas regiones del ultravioleta e infrarrojo medio, el vidrio absorbe mucha radiación y para los espesores que habitualmente se utilizan en los vidrios de las ventanas de las casas o de los automóviles, se absorbe casi toda la radiación incidente, proviniente por ejemplo del Sol y esa es la razón por la que no podríamos broncearnos tomando el sol detrás de una ventana con cristal, porque los rayos ultravioletas, responsables del bronceado, no son capaces de atravesar el vidrio de la ventana y quedan absorbidos en ella.
También ésta es la causa por la que el vidrio es un material apropiado para utilizarse en la construcción de invernaderos ya que permite el paso de la luz visible que aporta calor al interior del invernadero, pero no permite la salida de las radiaciones del infrarrojo, portadoras de calor, que son reflejadas o quedan atrapadas en el vidrio, aportando calor al sistema.
En todas las demás situaciones intermedias no se dispondrá de una aproximación que simplifique el cálculo y habrá que efectuar el mismo en la forma anteriormente descrita, integrando las expresiones numéricamente dentro del intervalo determinado por el ancho de banda espectral.
Además, si la incidencia no es normal, los materiales son absorbentes, o se necesita incluir una tercera o más superficies en el sistema, las expresiones algebraicas se complican mucho y el método expuesto resulta prácticamente inaplicable por lo que resulta sensato utilizar otro que permita realizar los cálculos de una forma más cómoda y asequible.
Con el uso de los ordenadores y máquinas automáticas de calculo resulta más sencillo utilizar algún método recurrente que pueda aplicarse a un sistema de múltiples superficies planas y paralelas y a radiación que incida bajo cualquier ángulo y con cualquier tipo de polarización.
Si consideramos un sistema como el de la figura siguiente, en el que las dimensiones transversales de las láminas se consideran mucho mayores que la dimension transversal del haz de radiación y la de éste a su vez mucho mayor que la longitud de onda, para poder evitar tener en cuenta los efectos de difracción, podemos ver las condiciones que cumplen las componentes del campo en cada lámina.

Siguiendo el método expuesto en (10), se consideran los promedios temporales de las funciones de onda en cada interfase y para el caso de incidencia normal la forma más general de los campos se puede expresar como la suma de dos ondas sinusoidales que se propagan en direcciones opuestas
Ei(z,t) = Ei(z) . ejwt = ejwt . [ Eti- + Eri- ]
en donde también se verifica que : Et(i-1)+ = Eti- . ejdi , y : Er(i-1)+ = Eri- . e-jdi , siendo di = 2.p.Ni .di /l , el espesor de fase de la capa i.
Estableciendo las condiciones de continuidad de los campos eléctrico y magnético en la interfase i, se tendrá :
Eti- + Eri- = Eti+ + Eri+
Ni . [ Eti- - Eri- ] = Ni+1 . [ Eti+ - Eri+ ]
Sustituyendo i por i-1 en estas ecuaciones y operando, obtenemos las relaciomes de recurrencia para las amplitudes de los campos transmitido y reflejado.
Eti-1- = 1/2 ( 1 + Ni/ Ni-1 ). Eti- . ejdi + 1/2 ( 1 - Ni/ Ni-1 ). Eri- . e-jdi
Eri-1- = 1/2 ( 1 - Ni/ Ni-1 ). Eti- . ejdi + 1/2 ( 1 + Ni/ Ni-1 ). Eri- . e-jdi
donde podemos tomar Etm+ = 1 , y Erm+ = 0 cuando el medio de emergencia es semiinfinito.
Teniendo en cuenta que :
Ei-1 = Eti-1- + Eri-1-
Hi-1 = Ni-1 . Eti-1- - Ni-1 . Eri-1-
y que : Eti- = 1/2 Ei + (1/2Ni) . Hi Eri- = 1/2 Ei - (1/2Ni) . Hi
ahora podremos expresar Ei-1 y Hi-1 en función de Ei y Hi .
Operando con las expresiones anteriores obtenemos :
Ei-1 = Ei . cos di + j (Hi / Ni) . sen di
Hi-1 = j Ni . Ei . sen di + Hi . cos di
expresiones que nos permiten calcular de forma recurrente los valores de los campos en las diferentes capas del sistema, partiendo de los valores en el medio de emergencia , Em = 1 , Hm = Nm+1
Las expresiones de la reflectancia y la transmitancia del sistema se pueden poner como:
R = |( E0 - H0 / N0 ) / ( E0 + H0 / N0)|2 T = 4 Nm+1 / ( N0 . | E0 + H0 / N0|2)
siendo N0 y Nm+1 los índices de refracción de los medios de incidencia y emergencia, respectivamente.
Para simplificar los cálculos se introduce el concepto de admitancia de la superficie i que se define como : Yi = Hi / Ei , la cual también debe cumplir las condiciones de continuidad en la superficie y cuyo cálculo recurrente a partir de las expresiones de Ei-1 y Hi-1 en función de Ei y Hi se puede escribir como :
Yi-1 = ( Yi + j Ni . tg di) / [ 1 + j (Yi / Ni) . tg di ]
Ahora podremos escribir la expresión de la reflectancia como :
R = |( N0 - Y0 ) / ( N0 + Y0 )|2 , poniéndola en función de la admitancia.
También para la transmitancia podemos obtener una expresión alternativa partiendo de su definición en función del vector de Poynting :
T = Ptm+ / Pt0- = (1 - R) . Pm / P0 = (1 - R) 1Pm (Pi / Pi-1) siendo :
Pi = Re [Ei . Hi] = |Ei|2 . Re [Yi] , por lo que de acuerdo con lo deducido en (10) se tendrá :
Pi / Pi-1 = (|Ni + Yi-1|2 . Re[Yi]) . e-2.Im(di) / (|Ni + Yi|2 . Re[Yi-1])
siendo Im(di) la componente imaginaria del espesor de fase de la capa i.
También se puede obtener una expresión para la energía absorbida dentro de la lámina i , llamada absorptancia de la lámina i , Ai , que se puede escribir como:
Ai = (Pi-1 - Pi) / Pt0- = (1 - R).(1 - Pi / Pi-1). 1Pi-1 (Pq / Pq-1)
la cual puede así también expresarse en función de la admitancia ,Y , en la superficie de las láminas.
Estas expresiones que han sido deducidas para el caso de incidencia normal pueden generalizarse para incluir el caso de incidencia bajo cualquier ángulo introduciendo los conceptos de índice de refracción efectivo y espesor de fase efectivo, con lo cual se podrán seguir utilizando las mismas expresiones sin más que sustituir en la expresión del espesor de fase, el índice de refracción Ni por el índice efectivo que ahora se puede poner como : Ni .cos bi , siendo :
cos bi = [ 1 - (N02 . sen2 a) / Ni2]1/2 con a = ángulo de incidencia
y sustituir Ni , en el resto de las expresiones, por Ni .cos bi en el caso de radiación polarizada perpendicularmente y por -Ni /cos bi en el caso de radiación polarizada paralelamente.
Las expresiones de la transmitancia y reflectancia en el caso de radiación incidente sin polarizar se podrán expresar como:
T = 1/2 ( Tp + Ts ) R = 1/2 ( Rp + Rs )
Para el caso de luz plano-polarizada a un ángulo z del plano de incidencia se tendrá :
T = Tp .cos2 z + Ts .sen2 z R = Rp .cos2 z + Rs .sen2 z
y para luz incidente polarizada elipticamente con amplitudes relativas as para la componente perpendicular, y ap para la dirección paralela, se tendrá;
T = (ap2 .Tp + as2 .Ts) / ( ap2 + as2 ) R = (ap2 .Rp + as2 .Rs) / ( ap2 + as2 )
en donde Ts , Tp , Rs y Rp son las transmitancias y reflectancias calculadas para polarización normal y paralela respectivamente.

SUPERFICIES LISAS Y RUGOSAS
Al hablar de superficies planas se hace referencia a superficies de dimensiones transversales grandes comparadas con las del haz de radiación que incide sobre ellas y cuyas posiciones medias pueden ser descritas, al menos localmente, por la ecuación de un plano, lo cual no supone necesariamente que dicha superficie tenga que ser también lisa, es decir que no pueda presentar pequeñas desviaciones con respecto al nivel medio, desviaciones que dan lugar a lo que es conocido con el nombre de rugosidad superficial, la cual hasta este momento no se ha tenido en cuenta para deducir las expresiones obtenidas.
La superficie que delimita un medio material puede ser vista como una interfase de transición entre dos medios, interfase que no es abrupta sino que en mayor o menor medida supone el paso gradual de uno a otro medio, con la existencia de estructuras atómicas o moleculares que se entrelazan creando campos de fuerza y gradientes de potencial que dependerán de la escala y de las características fisico-químicas de los materiales implicados.
Cuando se habla de superficies lisas o rugosas, siempre tendremos que admitir que la rugosidad de una superficie es un concepto relativo y así, superficies que a simple vista parecen lisas no lo son tanto cuando las observamos con mayor detalle haciendo uso de una lupa o microscopio con los aumentos adecuados.
En un medio con estructura amorfa o muy desordenada, como puede ser el caso de un líquido, la superficie que se presenta en contacto con un medio externo como el aire puede llegar a ser muy lisa en ausencia de vibraciones o de otros fenómenos que alteren su estado, ya que los átomos o moléculas del líquido son libres para deslizarse entre ellos lo que resulta en una interfase con estructuras de dimensiones muy pequeñas, comparables a las dimensiones atómicas o moleculares.
Si dicho medio se solidifica se produce, dependiendo de la forma en que se haga, una ordenación con o sin cristalización de los átomos y moléculas del mismo que resulta en la formación de estructuras rígidas cuyas dimensiones y orientación pueden dar lugar a que la interfase entre el medio solidificado y el medio que le rodea, la superficie de separación, presente una apariencia con facetas de dimensiones supramoleculares que configuran una mayor rugosidad superficial.
Ésta es sólo una posible forma en la que una superficie puede llegar a presentar rugosidad, pues otros fenómenos tales como la erosión física o química y el impacto de partículas pueden producir rugosidad en una superficie que era previamente más lisa, y en ocasiones así se produce de forma controlada en ciertas aplicaciones en las que se busca la mayor utilidad que una superficie con cierto grado de rugosidad presenta frente a una que no la tiene, como es el caso, por ejemplo, de la rugosidad superficial o textura que se produce en algunas células solares fotovoltaícas con el objetivo de disminuir la cantidad de luz reflejada en su superficie y aumentar así su rendimiento de conversión de energía, y también el de las superficies que se usan en algunas pantallas de televisión y monitores de ordenador que se fabrican con un cierto grado de rugosidad superficial controlada con el objeto de disminuir las molestas reflexiones y brillos que se producen en una superficie muy lisa y mejorar así las condiciones de visibilidad de las mismas.
Estos son sólo dos ejemplos pero hay muchos otros en los que un cierto grado de rugosidad superficial puede resultar útil y también por contra puede haber situaciones en las que la rugosidad superficial de un medio puede resultar inconveniente para algún tipo de aplicación o fenómeno físico que deseemos utilizar o estudiar, por ello es interesante saber cómo y en que medida tiene influencia un cierto grado de rugosidad superficial sobre los fenómenos de reflexión, transmisión y absorción de la radiación electromagnética en los medios materiales.
El tema tiene interés en muchos campos, desde la reflexión de ondas de radio en la superficie del mar hasta la detección por radar de microondas reflejadas en diversos tipos de superficie, entre otros, y por ello ha sido estudiado por muchos investigadores desde diversos puntos de vista aunque todos ellos coinciden en señalar que dada la variedad de los procesos que pueden generar rugosidad en una superficie, no puede existir un único tratamiento matemático aplicable a todas las posibles situaciones que se presenten en la realidad.
Si exceptuamos el caso de las irregularidades periódicas, cuya variación con respecto a las coordenadas x e y puede ser descrita por una función matemática periódica de propiedades conocidas, caso de las redes de difracción y texturas similares, el resto de las superficies rugosas se generan en su gran mayoría como consecuencia de procesos aleatorios y por ello las posiciones de la superficie y su desviación respecto del nivel medio no pueden describirse por funciones explícitas y sólo son tratables desde un punto de vista estadístico.
La presencia de rugosidad superficial tiene influencia sobre la forma en que la radiación electromagnética se refleja y se transmite en la superficie entre dos medios materiales produciendo efectos nuevos, no considerados hasta ahora, tales como la difusión de parte de la luz incidente en direcciones distintas a las previstas por las leyes de Snell, la posible presencia de absorción en la interfase y la modificación de los valores de los coeficientes de reflexión y transmisión con respecto al caso de la superficie lisa.
Se comprueba experimentalmente que estos efectos presentan una dependencia fuerte con respecto a la longitud de onda de la radiación incidente, lo que conduce en la práctica a que superficies que se comportan como lisas para radiaciones de ciertas longitudes de onda, como por ejemplo las ondas de radio, presenten un efecto muy marcado de rugosidad cuando se iluminan con radiaciones de longitudes de onda menores, como por ejemplo las del infrarrojo o el visible.
Así se recoge en algunas de las aproximaciones al problema, como las de Davies, Bennet y Porteus (11), en las que se caracteriza la superficie a través de dos parámetros estadísticos, la amplitud cuadrática media de las irregularidades, s , y la pendiente cuadrática media de las mismas, p , definidas dentro de una cierta distancia media de correlación, a , que, cuando se imponen ciertas condiciones a la superficie tales como que la distribución de las alturas de las irregularidades y la de las pendientes sean normales o Gaussianas alrededor del valor medio y que la superficie sea estacionaria e isotrópica con respecto a la posición a través de ella, se llegan a definir de la siguiente forma :
s = h /(2)1/2 p = ± (2)1/2.s /a a2 = [2/(s)2]  S . A(S) . dS S . A(S) . dS
donde h es la amplitud máxima de las irregularidades dentro de la distancia de correlación , a , y S y A(S) son la proyección de la distancia entre dos puntos de la superficie sobre el plano medio y la función de autocovarianza de los mismos, respectivamente.
Con estas condiciones y suponiendo además que s es mucho menor que la longitud de onda de la radiación incidente y que el radio de curvatura de las irregularidades es grande con respecto a la longitud de onda, lo cual supone que la distancia de correlación , a , sea también mayor que l, es posible aplicar el método de difracción de Kirchoff a la reflexión de radiación electromagnética en dicha superficie y se obtiene, para la expresión de la reflectancia en el caso de incidencia normal desde el aire :
Rs = R0 . e-(4 p s)2 / l2
siendo R0 la reflectancia de una superficie lisa del mismo material y Rs la reflectancia en la dirección especular de la superficie con rugosidad.
La extensión de este tratamiento (12) a incidencia bajo un ángulo cualquiera , a , y medio de incidencia con índice de refracción N0 da como resultado la expresión :
Rs = R0 . e-(4 p N0 s cos a)2 / l2
La comprobación experimental de esta expresión, llevada a cabo para incidencia casi normal sobre superficies de vidrio finamente pulidas y recubiertas de una capa de aluminio, mostró buen acuerdo con la teoría, tal y como puede verse en la figura siguiente, reproducida de la referencia (11).

En la figura los puntos corresponden a medidas experimentales, la linea continua a el cálculo obtenido para incidencia normal con la anterior expresión y la linea de trazos corresponde a el cálculo corregido asumiendo que una parte de la radiación recogida en el detector es también radiación difundida que entra dentro del ángulo de aceptación del mismo , Dq , según la expresión para la dependencia angular de la radiación difractada en el caso de incidencia normal:
rd(q) dq =
R0 .2.p4.(a /l)2. (s /l)2.(cos q + 1)4.sen q. e[-(p a. sen q)2 /l2].d q
Rs = R0 . e-(4 p s)2 / l2 + R0 . (25.p4 /p2) . (s /l)4. (Dq)2
Expresiones que dado el carácter isotrópico de la superficie considerada pueden generalizarse, tentativamente, para ángulos de incidencia , a , próximos a la normal a :
rd(q) dq =
R0 .2.p4.(a /l)2. (s . cos a /l)2.(cos q + 1)4.sen q. e[-(p a. sen q)2 /l2].d q
Rs = R0 . e-(4 p s .cos a)2 / l2 + R0 . (25.p4 /p2) . (s .cos a /l)4. (Dq)2
También se puede ver en la figura que para valores de la reflectancia especular menores de aproximadamente .75 el calculo corregido se vuelve a desviar de las medidas experimentales, hecho que los autores atribuyen a que para esas longitudes de onda menores ya no se cumplen las hipótesis bajo las que el tratamiento matemático desarrollado resulta válido.
La extensión de los resultados encontrados para la reflexión se ha intentado hacer (13), suponiendo las mismas condiciones, al caso de la radiación transmitida por una superficie rugosa encontrándose para la transmitancia en la dirección especular una expresión análoga a la encontrada para la reflectancia, que en el caso de incidencia normal se expresa por :
Ts = T0 . e -[ 2 p s (N - N0) /l ]2
y que para un ángulo de incidencia, a , con respecto a la normal toma la forma :
Ts = T0 . e -[ 2 p s (N - N0) cos (a) /l ]2
donde N0 y N son los índices de refracción del medio de incidencia y del medio incidido y Ts y T0 son las transmitancias en la dirección especular de la superficie con rugosidad y de una superficie idealmente lisa del mismo material, respectivamente.
En el caso de la transmisión en una lámina o sistema de láminas, no es tan inmediato como en el de la reflexión en una superficie metálica el poder hacer una estimación de la cantidad de radiación difundida que es recogida dentro del ángulo de aceptación del detector, ya que dependerá en cada caso particular del espesor de la capa o capas que haya detrás de la superficie rugosa, del número de éstas y de sus índices de refracción (14).
Lo mismo puede decirse de la radiación reflejada fuera de la dirección especular por un sistema de láminas débilmente absorbentes cuya primera superficie presenta un cierto grado de rugosidad.
En estos casos en que intervienen tantos factores serían más adecuadas expresiones empíricas del tipo :
Rs = R0 . e-[4 p N0 sef cos (a) / l](1+b) , , Ts = T0 . e -[ 2 p sef (N - N0) cos (a) /l ](1+b)
en donde sef representa un valor efectivo de la amplitud cuadrática media de las irregularidades de la rugosidad superficial y b es un parámetro cuyo valor puede estar comprendido entre 0 y 1.
Las expresiones aquí presentadas facilitan mucho el cálculo de los valores de transmitancia y reflectancia especulares correspondientes a una superficie con cierto valor de rugosidad conocido a través de dos parámetros sencillos, como son el valor cuadrático medio de la amplitud de las irregularidades, s , y la pendiente cuadrática media de las mismas, p , dentro de la distancia de correlación, a , ya que los relacionan con los valores de transmitancia y reflectancia de la respectiva superficie lisa, cuyas expresiones se conocen y se pueden calcular en función de las propiedades del material y de la radiación incidente para cada caso concreto.
No obstante, las condiciones que se han impuesto para la obtención de dichas expresiones son bastante restrictivas y limitan su aplicación al caso de superficies únicas en las que las pendientes de las irregularidades son muy pequeñas, evitando así la necesidad de tener en cuenta el efecto de la múltiple difusión o scattering que podría tener lugar entre facetas muy próximas entre sí, cuando la distancia de correlación no cumpliera con la condición de ser mucho mayor que la longitud de onda, y tampoco tienen en cuenta el efecto de la interferencia en sistemas de láminas, que modifica significativamente la cantidad de radiación desviada fuera de la dirección especular.
Además se exige para poder aplicar dichas expresiones que la amplitud cuadrática media de las irregularidades sea mucho menor que la longitud de onda y esto limita su posible aplicación a valores de rugosidad pequeños frente a la longitud de onda de la radiación utilizada, lo cual no siempre se cumple cuando se trata con superficies rugosas de todo tipo.
De todas las condiciones exigidas para la obtención de estas expresiones, quizá la menos restrictiva sea la de suponer que las distribuciónes de las amplitudes y las pendientes de las irregularidades siguen una ley normal o Gaussiana con respecto al valor medio de las mismas, ya que como se ha dicho son muchos los casos en los que la rugosidad superficial aparece como consecuencia de un proceso aleatorio y en tal circunstancia es altamente probable que muchas de las superficies rugosas así generadas cumplan con dicha condición y también en muchos de ellos con la de ser isotrópicas.
Algunas de las superficies que se encuentran en la realidad pueden considerarse ajustadas a las condiciones impuestas, superficies con rugosidad suave de tipo onduladorio sin picos ni valles escarpados, y a ellas serían aplicables las expresiones anteriores, pero también son muchas las superficies que presentan una rugosidad con irregularidades muy cercanas unas de otras, con pendientes abruptas como las mostradas en la figura siguiente, que ofrece fotografías tomadas con microscopio electrónico de barrido, reproducidas de la referencia (15), en las que los fenómenos de difusión múltiple de la luz entre las facetas superficiales no pueden ser ignorados y para las cuales no serían directamente aplicables las expresiones deducidas.
 |  |
El efecto más evidente que una superficie con cierto grado de rugosidad tiene sobre la reflexión y la transmisión de la radiación electromagnética que incide sobre ella es, como se ha mencionado, el de producir difusión de parte de la radiación incidente y disminuir la fracción de luz que se refleja y transmite siguiendo la dirección especular o prevista por las leyes de Fresnel, por ello una superficie lisa puede devolver una imagen especular de un objeto o transmitir una imagen nitida del mismo mientras que una superficie rugosa devolverá una imagen borrosa o distorsionada, o en casos extremos no devolverá imagen especular alguna y sólo se podrá apreciar una imagen de la propia superficie.
Esta observación está de acuerdo con lo previsto por las expresiones anteriormente expuestas en las que un aumento del parámetro s , que va asociado a una rugosidad mayor, determina una disminucion de los valores de la reflectancia y transmitancia en la dirección especular, por ello suponemos que dichas expresiones podrían ser también válidas para superficies que no cumplan estrictamente con las condiciones que se han impuesto para su deducción, siempre que se superen las contradicciones que se producen entre las hipótesis adoptadas y las propiedades de las superficies reales a las que se pretende aplicar el método utilizado.
Una de las aproximaciones que se realizan para llegar a obtener las expresiones que relacionan la reflectancia especular con la reflectancia de la superficie lisa es considerar que el valor medio de la reflectancia de la superficie rugosa se puede obtener integrando la reflectancia correspondiente a cada uno de los puntos de la superficie a lo largo y ancho de ella y asumir que el resultado coincide con la reflectancia correspondiente a la altura y pendiente medias de las distribuciónes de alturas y pendientes, que al considerarse Gaussianas se supone que coinciden con x(x,y) = 0 , p = 0 , y puede considerarse que entonces dicha reflectancia es la misma que la que tendría la superficie lisa, R0 , para cada ángulo de incidencia , a .
Esta aproximación, que se muestra bastante acertada cuando las irregularidades de la superficie son pequeñas y varían lentamente con pendientes pequeñas a lo largo y ancho de la sección de incidencia del haz de radiación, no parece que pueda ser aplicada cuando las variaciones son más abruptas ya que en este caso es probable que la onda reflejada lo sea despues de haber sufrido más de una reflexión en las facetas de la rugosidad, habiéndose podido producir alguna absorción en la interfase y habiéndose modificado sensiblemente los coeficientes de reflexión y de transmisión de dicha interfase con respecto a los de la superficie lisa.
Por otra parte el tratamiento matemático podría mantenerse, siempre que adaptemos la reflectancia que se utiliza en el mismo a la que se presenta en la situación real y esto puede hacerse por medio de un modelo que considere la interfase como un sistema de láminas paralelas con el número de capas adecuado, cada una de ellas con un factor de empaquetamiento de masa proporcional a la distribución de volumen correspondiente al de la superficie rugosa dentro de ese nivel de alturas y cuyo índice de refracción se calcule en función del índice de refracción de los dos medios, el de incidencia N0 = n0 - jk0 , y el del material incidido Nf = nf - jkf , respectivamente, y de el correspondiente factor de empaquetamiento de masa , xi , dentro de cada capa i, de acuerdo con las expresiones siguientes :
ni = n0(1 - xi) + nf xi ki = k0(1 - xi) + kf xi
Con este modelo se pueden tener en cuenta efectos como las múltiples reflexiones en las facetas de la rugosidad, la posible absorción dentro de ellas y además proporciona valores de la reflectancia y la transmitancia promediados y uniformes, que son adecuados para ser integrados en la aplicación del método de Kirchoff que conduce a la obtención de la función característica que afecta a dichos valores de reflectancia y transmitancia para la obtención de los correspondientes en la dirección especular.
Rs = Rm . e-[4 p N0 sef cos (a) / l ](1+b) Ts = Tm . e -[ 2 p sef (N - N0) cos (a) / l ](1+b)
donde Rm y Tm son la reflectancia y transmitancia, respectivamente, calculadas con el modelo mencionado, y Rs y Ts son al igual que antes la reflectancia y transmitancia en la dirección especular, respectivamente.
Un tipo de modelo similar ha sido utilizado para describir por sí solo el comportamiento óptico de superficies altamente texturadas (16,17), considerando un número muy grande de capas en las que la difracción de la radiación se supone que tiene lugar en múltiples pequeñas partículas distribuidas dentro de ellas de acuerdo con diferentes patrones de densidad, según el tipo de superficie que se quiere modelar.
En el modelo que aquí se utiliza se supone que las capas están compuestas de un material homogéneo e isótropo, caracterizado por su índice complejo de refracción, siendo el número de capas pequeño y dependiente del valor de los parámetros con los que describimos la rugosidad, es decir de la amplitud cuadrática media de las irregularidades y de la distancia media de correlación entre ellas.
Así, para un mismo valor de la amplitud cuadrática media de las irregularidades en dos superficies que sólo se diferencian entre sí en la forma en que dichas irregularidades están distribuidas o en la pendiente de las mismas, se podrá tener en cuenta esta variación entre ambas a través de incluir diferente número de capas en uno y otro caso, obteniendo de esta forma resultados distintos para cada una de ellas.
Puede verse en la figura siguiente, en la que una superficie rugosa se ha representado en dos dimensiones por simplificar, que a lo largo del doble de la distancia promedio de correlación , a , se recorrerían todas las alturas de la distribución gaussiana de las irregularidades cuya amplitud cuadrática media y amplitud máxima son s y h , respectivamente, y también se recorren todas las pendientes de uno y otro signo de la distribución correspondiente.

En la parte central de dicha figura se pueden ver representadas las pendientes medias de la distribución, definidas como h/a y -h/a respectivamente y también, superpuesta, una función senoidal del tipo z=(h/2)[1+sen (py/a)] que cumple con la misma condición de que el valor "eficaz" o cuadrático medio de sus amplitudes dentro del intervalo [0,2a] es h/(2)1/2, cuyas pendientes medias también coinciden con las de la distribución normal y que puede servir para calcular los factores de empaquetamiento de masa de las capas correspondientes a cada altura en el modelo.
En la parte inferior de la figura se ha sustituido, para este mismo caso, la superficie rugosa por dos capas con índices de refracción determinados por el factor de empaquetamiento de masa dentro de cada una de ellas, correspondiente al volumen de cada uno de los dos medios, incidente e incidido, que esté incluido en ese intervalo de alturas en la superficie rugosa considerada.
El número de capas a incluir en el modelo vendrá determinado en cada caso por las características de la superficie rugosa a la que debe sustituir, que en principio pueden venir definidas por los dos parámetros s y a , o alternativamente por la amplitud máxima de las irregularidades, h , y la distancia de correlación entre ellas, a .
En un extremo tendremos los casos de superficies con facetas de las irregularidades que presentan pequeñas pendientes o valores pequeños de la relación h/a y en este caso el número de capas a incluir en el modelo será cero, ya que en este caso son directamente aplicables las expresiones deducidas teniendo en cuenta dicha hipótesis de pendientes pequeñas.
Para asignar algún valor a este límite inferior de dicha relación, h/a , se supone, por analogía con la óptica geométrica, que para los valores de h/a <= 1/2 , ó teniendo en cuenta el ángulo de incidencia, (h.cos a) /a <= 1/2 , el efecto de las múltiples reflexiones entre facetas es despreciable y por tanto no tenemos que incluir ninguna capa en el modelo.
A partir de este valor y para valores superiores de la relación (h.cos a) /a , se incrementa el número de capas del modelo en una capa por cada incremento del valor de dicha relación en una unidad, es decir una capa para valores de hasta 3/2, dos capas para valores de hasta 5/2, tres capas para valores de hasta 7/2 y cuatro capas para valores superiores, valor por encima del cual el efecto adicional de nuevas capas produce mínimos efectos en los resultados calculados con el modelo y que es una situación que correspondería a superficies altamente texturadas, con irregularidades muy próximas unas de otras, marcando el otro extremo en las características de las superficies que se pueden presentar en la realidad.

MEDIDAS Y SIMULACION NUMERICA
Una de las ventajas que tiene el trabajar con funciones como la reflectancia y la transmitancia es que se han definido como magnitudes relativas, es decir se obtienen de la comparación entre las intensidades de la radiación reflejada o transmitida, respectivamente y la intensidad incidente, lo cual permite prescindir del uso de patrones absolutos para medir el valor de dicha intensidad de la radiación en cualquiera de sus formas.
Una forma elemental de realizar este tipo de medidas consiste en situar un detector de radiación del tipo adecuado delante de la fuente de radiación y registrar la lectura que en él se produce y a continuación interponer entre la fuente y el detector el material que queremos medir, registrando la nueva lectura del detector cuyo cociente con respecto a la anterior permitiría obtener el valor de la transmitancia en este caso (ver figura).
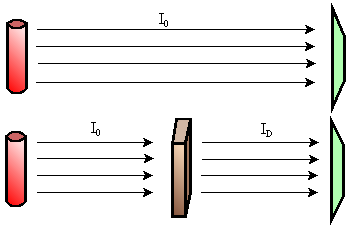
Si se quisiera medir la reflectancia habría que cambiar la posición del detector de forma que la radiación que ahora recibiera fuese la reflejada por el material bajo ensayo, manteniendo la misma distancia en la trayectoría que recorre la radiación entre fuente y detector que en ausencia de la muestra de material.
Las fuentes de radiación electromagnética emiten dicha radiación distribuida dentro de un cierto rango de longitudes de onda, con intensidad que varía dependiendo de cada longitud de onda y que puede ser descrita por una función I(l) , por lo que la intensidad total emitida por la fuente se podrá expresar como :
I0 =  I(l) . dl I(l) . dl
donde la integración se extiende entre cero e infinito aunque en la mayor parte de los casos será suficiente con integrar en el intervalo comprendido entre dos valores de la longitud de onda , l1 y l2 , fuera del cual la intensidad emitida por la fuente puede considerarse prácticamente nula.
En estas condiciones la señal generada por un detector que recibe la intensidad I0 será proporcional a dicha intensidad y si la respuesta del detector es lineal, la señal generada por una intensidad I0 /2 será también la mitad de la señal anterior.
Por ello, si entre la fuente y el detector se ha interpuesto un material cuya transmitancia es T , la señal generada en el detector será proporcional a la intensidad ID= I0.T y este será un dato que proporciona información sobre el total de intensidad transmitida por ese material para esa fuente de radiación, pero no facilita información sobre qué parte de esa radiación recogida en el detector pertenece a una u otra zona del rango de longitudes de onda de la radiación emitida por la fuente.
Son muchas las causas por las que el valor de la transmitancia de un material puede depender de la longitud de onda de la radiación incidente y entre ellas se tienen los efectos de interferencia en láminas delgadas, la dependencia del índice complejo de refracción del material con dicha longitud de onda y los fenómenos de difracción y difusión en superficies rugosas, entre otras, por lo que T no será por lo general una constante sino que se podrá expresar como una función T(l) que tiene en cuenta dichos efectos.
Aceptando esto, la intensidad total recogida en el detector se puede poner como :
ID =  I(l) . T(l) . dl I(l) . T(l) . dl
y la señal generada en el detector será proporcional a dicha intensidad recibida.
¿Qué ocurre cuando la fuente utilizada emite radiación que es monocromática o casi monocromática con un ancho de banda , Dl , muy pequeño alrededor de una longitud de onda central , l m ?
En este caso el intervalo de integración es muy pequeño y si es lo suficientemente pequeño para considerar que T(l) es constante en todo el intervalo, con el valor correspondiente a la longitud de onda media del intervalo, lm , la anterior expresión de ID se puede aproximar ahora por : ID = I0.T(lm) , siendo I0 al igual que antes la intensidad de la radiación emitida por la fuente, que en este caso estará comprendida dentro de un estrecho rango de longitudes de onda.
La información ahora obtenida se refiere sólo a una longitud de onda o a un intervalo muy pequeño de ellas, por lo que si se utilizaran muchas fuentes casi monocromáticas de diferentes longitudes de onda se podría obtener información sobre como se comporta la transmitancia del material bajo ensayo para diferentes valores de la longitud de onda y esa información es lo que comunmente se conoce con el nombre de espectro de transmisión si se registra el valor de la transmitancia o espectro de reflexión , si se registra el valor de la reflectancia.
Esta información es muy útil y tiene múltiples aplicaciones prácticas, por ello y a falta de un número suficiente de tales fuentes monocromáticas se ha buscado obtenerlas utilizando dispositivos que permiten seleccionar una pequeña parte del espectro obtenido al separar espacialmente la radiación no monocromática emitida por una fuente, en las diferentes longitudes de onda o colores que la componen.
Los métodos utilizados para conseguir esto han sido muy variados, desde la utilización de filtros selectivos que dejan pasar sólo radiación de una cierta franja de longitudes de onda, hasta la utilización de los llamados monocromadores, basados en prismas de diferentes materiales o en redes de difracción y el uso de interferómetros y otros dispositivos que buscan el mismo objetivo.
Desde el descubrimiento del prisma se ha venido utilizando este elemento para la observación de espectros de diferentes tipos, de transmisión de materiales y también de emisión de distintas fuentes de radiación, usando unos dispositivos llamados espectroscopios, consistentes básicamente en un tubo dotado de rendijas para colimar y limitar la radiación de entrada, un prisma de vidrio o cuarzo sobre el que se hace incidir la radiación proviniente de las rendijas de entrada y otro tubo situado a un ángulo adecuado y provisto de rendijas para colimar la radiación de salida del prisma y observar a través de un orificio el espectro formado.
Con el posterior desarrollo de los detectores electrónicos de radiación y la electrónica de medida y control asociada a los mismos, se puso de manifiesto la posibilidad de realizar medidas de intensidad de radiación con mayor precisión y exactitud, dando lugar a un nuevo tipo de instrumento formado por la combinación de una fuente de radiación, un monocromador y un detector de radiación, el conocido como espectrofotómetro.
Uno de los primeros modelos de espectrofotómetro que se comercializó en la década de los años 1950 fué el Beckman DU cuyo esquema óptico se muestra en la figura siguiente, reproducida de la referencia (18).

En la figura se pueden ver varios aspectos interesantes que incorporaba este instrumento de medida que utilizaba como fuente de serie una lámpara de tungsteno, aunque ofrecía la posibilidad de utilizar alternativamente una lámpara de hidrógeno para realizar medidas en el ultravioleta.
Utilizaba un espejo semitransparente para dirigir la radiación de la fuente hacia la rendija de entrada y basaba su poder resolutivo en el largo camino recorrido por la radiación una vez refractada en el prisma utilizado como elemento dispersor del monocromador.
Éste era de cuarzo, lo cual permitía trabajar con él en la región del ultravioleta, y de base recta con una superficie trasera aluminizada con lo que se consigue un mayor camino en la refracción de la luz y al mismo tiempo compensar los efectos de polarización que introduce el cuarzo sobre dicha radiación refractada, radiación cuya longitud de onda se selecciona a través de un mecanismo que permite girar el prisma con mucha precisión obteniendo las lecturas en una escala rotatoria adecuadamente graduada.
Tanto la radiación incidente como la dispersada se dirigen mediante un espejo colimador y, a la salida, la radiación de la longitud de onda seleccionada atraviesa el espejo semitransparente y posteriormente la posición en la que se puede situar la muestra, antes de llegar al detector que utiliza un fotomultiplicador como elemento sensible.
El proceso de medida con este instrumento consistía básicamente en seleccionar primero la longitud de onda a la que se iba a medir, realizar un ajuste del cero de transmitancia para lo cual se colocaba un bloque opaco en la posición de muestra y se ajustaba la lectura del galvanómetro a cero, se extraía despues el bloque dejando libre la posición de muestra y se ajustaba la lectura del galvanómetro al 100% o 1 de transmitancia, procediendo a continuación a colocar la muestra en su posición y realizar la lectura de la transmitancia en el galvanómetro.
Este proceso se realizaba para cada longitud de onda para la que se deseara medir la transmitancia, por lo que obtener un espectro de transmisión consistente en medidas a 10 o 12 longitudes de onda diferentes representaba una lenta y ardua tarea, teniendo en cuenta las necesarias repeticiones debido a oscilaciones en la intensidad de la fuente de radiación, variaciones en las lecturas del detector y otras dificultades que solían surgir muy frecuentemente.
Muchas de las dificultades experimentadas con este tipo de instrumentación provenían de la rudimentaria electrónica utilizada en su construcción, basada en tubos de vacío y medidores de aguja, como el galvanómetro, que no permitían una buena estabilidad y precisión en las medidas, pero esto cambió radicalmente en las décadas siguientes con el rápido desarrollo de la electrónica de semiconductores, el perfeccionamiento de los componentes ópticos y de los detectores y fuentes de radiación electromagnética utilizados, que dieron paso a una nueva generación de instrumentos mucho más precisos y cómodos de usar.
Al mismo tiempo y basándose en estos estos avances en la fabricación de componentes se desarrollaron nuevos conceptos en el diseño de los espectrofotómetros, siendo uno de los más notables el sistema de doble haz, mediante el cual se miden alternativamente y de forma automática las intensidades de radiación que pasan directamente y a través de la muestra al detector, realizando automáticamente el ajuste de cero y el cálculo de la transmitancia, obteniendo su lectura en displays o presentadores digitales que permiten una mayor precisión en la lectura de los valores medidos.
Estos desarrollos, junto con la utilización de nuevas fuentes y detectores de radiación, permitieron la construcción de diferentes tipos de espectrofotómetros cubriendo todo el rango de longitudes de onda desde 180 nm en el ultravioleta hasta 50 mm en el infrarrojo medio, dentro de las frecuencias ópticas.
El sistema de doble haz se ha incorporado en casi todos los nuevos modelos de espectrofotómetros, los cuales utilizan en su mayoría redes de difracción como elemento dispersivo en combinación con filtros o prismas para eliminar los órdenes superiores de difracción lo que, unido al uso de rendijas variables, permite reducir mucho la anchura de banda de la radiación obtenida a la salida del monocromador, como es el caso en el espectrofotómetro modelo 340 de Perkin-Elmer cuyo esquema óptico se ofrece en la figura siguiente, reproducida de la referencia (19).
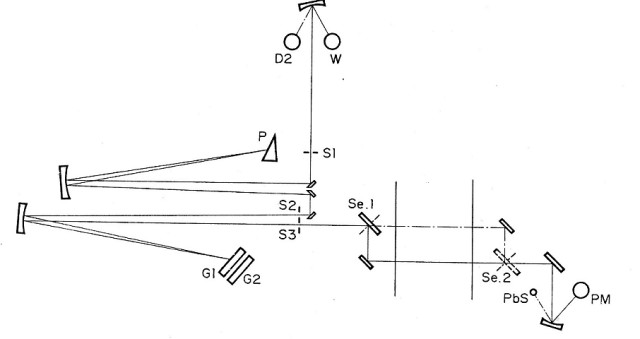
En la figura se puede ver que en este caso se utiliza un prisma como elemento dispersor previo al uso de una red de difracción, la cual en este modelo es seleccionable entre dos, según los valores de longitudes de onda en que se trabaje, ya que este modelo podía medir en todo el rango comprendido entre 180 nm y 2600 nm, para lo cual disponía también de dos fuentes de radiación, una lámpara de deuterio para el ultravioleta y una lámpara de tungsteno para la región del visible y del infrarrojo próximo, y también disponía de dos detectores, un fotomultiplicador para el ultravioleta y visible y una célula de sulfuro de plomo para el infrarrojo próximo.
El intercambio de las redes de difracción, así como de los detectores se realiza automáticamente y el sistema de doble haz se implementa por medio de dos espejos rotatorios sincronizados, que dirigen el haz de radiación monocromática alternativamente, varias veces por segundo, a través de una posición ocupada por la muestra y a través de otra que puede permanecer libre o puede ocuparse con una compensación o "blanco" adecuado y disponen de un tercer sector que bloquea el paso de radiación para así poder ajustar la lectura de cero.
El uso de motores paso a paso para mover los elementos dispersores y el control por microprocesador de todo el funcionamiento de estos equipos, hace posible obtener un espectro de transmisión contínuo dentro de un amplio rango de longitudes de onda, por ejemplo en toda la región del visible, en unos pocos minutos y la utilización de registradores en papel y de impresoras permite su obtención gráfica en una escala graduada.
Al igual que sucede en otro tipo de instrumentos de medida, la incorporación del uso de ordenadores para el control del funcionamiento de los espectrofotómetros facilita también la toma automática de lecturas a longitudes de onda preseleccionadas y la utilización de los valores medidos para obtener otros parámetros cuyo cálculo ha sido programado previamente.
Al mismo tiempo se han desarrollado accesorios para adaptarlos fácilmente a los espectrofotómetros y poder realizar otro tipo de medidas, como son las medidas de reflectancia especular y también de reflectancia total, así como la posibilidad de extraer el haz de radiación por medio de fibras ópticas para realizar medidas sobre materiales en el exterior del espectrofotómetro o la adaptación de microscopios que permiten obtener espectros sobre fracciones muy pequeñas del material bajo estudio.
Por todo ello el espectrofotómetro es un instrumento muy adecuado para la realización de medidas de transmisión y reflexión en todo tipo de materiales, su uso está muy extendido en los laboratorios de análisis físico-quimicos y también tiene mucha aplicación en los laboratorios biológicos y farmaceúticos.
Su campo de aplicación es tan amplio que ha motivado que, además de las medidas básicas de transmitancia, se haya dotado a los espectrofotómetros de otras capacidades tales como la obtención de una función calculada a partir de la transmitancia, la llamada Absorbancia, definida como el logaritmo decimal de la inversa de la transmitancia y cuya obtención es conveniente para aplicarla en los procesos de cuantificación de analitos en disolución que se llevan a cabo en el análisis químico, cuya absorción de la radiación se puede describir adecuadamente por medio de la llamada ley de Bouguer-Beer-Lambert , que se expresa como : A = a . d . c , siendo A la absorbancia, a la llamada absortividad del soluto, d el espesor recorrido por la radiación y c la concentración del soluto en la disolución.
Otras posibilidades que ofrecen los espectrofotómetros actuales son la obtención de las derivadas hasta el tercer y cuarto grado de la transmitancia y de la absorbancia asi como, consecuencia de su uso conjunto con el ordenador, su aplicación a la cuantificación de mezclas por medio de ajustes multipunto a diferentes longitudes de onda preseleccionadas.
Asi pues, el método de medida más eficaz para la obtención de los valores de transmitancia y reflectancia de materiales es por medio del uso de un espectrofotómetro que pueda trabajar en la región de longitudes de onda de interés y que permita seleccionar algunos de los parámetros que pueden tener influencia sobre dichos valores medidos, como son por ejemplo el ancho de banda y el rango de las longitudes de onda de la radiación utilizada en la medida.
Por ejemplo, una medida sencilla que permite comprobar la validez del
cálculo realizado anteriormente para obtener el valor de la transmitancia de una lámina de vidrio de caras paralelas, cuyo índice de refracción sea N = 1.5 y no absorba radiación, para el cual se obtuvo un valor de T = .923, se presenta en la figura siguiente en la que se ha obtenido un registro gráfico de la medida de la transmitancia, en incidencia normal, de una lámina de vidrio de 1 mm de espesor, de las usadas como porta-objetos en los microscopios, y cuyo índice real de refracción es aproximadamente constante e igual a 1.5 en todo el rango de longitudes de onda explorado, que en este caso va desde 550 nm a 850 nm.

El ancho de banda de la radiación utilizada en esta medida se ha seleccionado a 2 nm , el tiempo que duró el registro de todo el espectro fue de 1 minuto aproximadamente y el espectrofotómetro utilizado en ésta y las siguientes medidas fué un UV-500 de Thermo-Unicam.
En la figura observamos que el valor de la transmitancia registrada se mantiene constante en el intervalo de longitudes de onda seleccionado y su valor es de aproximadamente T = .920 , el cual está en muy buen acuerdo con el valor calculado , .923 , si tenemos en cuenta que es posible que haya una pequeña absorción en el material, que no se ha considerado en los cálculos, y que el índice de refracción cuyo valor se ha tomado como 1.5 puede que no sea exactamente ese y difiera de él ligeramente.
También se puede ver en la anterior figura que el valor de la transmitancia no presenta prácticamente ninguna dependencia con respecto a la longitud de onda, de lo cual podríamos concluir que las dos superficies de la lámina son muy lisas y también que el índice de absorción, k, en caso de que no sea cero debe de tener un valor muy pequeño.
El hecho de que no se observen efectos de interferencia en la figura es consecuente con las características de la lámina y de la radiación utilizada en la medida, ya que la mayor longitud de coherencia de la radiación a la longitud de onda de 850 nm , siendo el ancho de banda de 2 nm, sería de 3.61 . 105 nm aproximadamente, mientras que el espesor de fase de la lámina, N.d , será de aproximadamente 1.5 . 106 nm, el cual es al menos cuatro veces mayor que la longitud de coherencia de la radiación y en consecuencia los efectos de interferencia resultan promediados y no se observan en el espectro registrado.
En este caso, debido a que no existe dependencia con la longitud de onda, la simulación del espectro de transmisión se limita a realizar el cálculo de la transmitancia en función de los índices reales de refracción de los medios de incidencia y emergencia y el de la lámina
, utilizando la expresión que se ha deducido anteriormente : T = T1 T2 /(1- R22), donde T1 y T2 son las transmitancias de la primera y segunda superficie respectivamente, y R2 es la reflectancia de la segunda superficie, que se calculan en función de los índices de refracción de los medios de incidencia y emergencia, en este caso el aire cuyo índice de refracción tomamos como de valor 1, y del índice de la lámina, que en este caso es de vidrio con N2 = 1.5 aproximadamente.
De esta forma, a partir de las fórmulas de Fresnel, estos valores de reflectancia y transmitancia de las interfases vendrán dados por :
R2 = [(N1 - N2) / (N1 + N2)]2 y T1 = T2 = 4 N1.N2 /(N1 + N2)2
de las que operando con los valores N1=1 y N2=1.5 , se obtiene el valor de T = .923 anteriormente mencionado.
Estos cálculos se pueden realizar de forma automática utilizando el programa de cálculo de la Transmitancia de una lámina gruesa
Si se quiere realizar la simulación del espectro de transmisión para una lámina cuyo índice de refracción no permanece constante en el rango de longitudes de onda considerado, el valor de la transmitancia variará en función de la longitud de onda y deberá calcularse para cada longitud de onda de interés dentro del espectro que se quiere simular.
Tal es el caso cuando por ejemplo se registra el espectro de una lámina de polimetil-metacrilato, conocido comercialmente como vidrio acrílico, de caras plano-paralelas y de 3 mm de espesor, en el rango de longitudes de onda comprendido entre 350 y 800 nm, el cual puede verse en la figura siguiente.

En este caso el índice de refracción entre 500 nm y 800 nm varía entre 1.496 y 1.484 aproximadamente, de acuerdo con la referencia (20), por lo cual podríamos hacer en dicha región una aproximación similar al caso de la lámina de vidrio, considerando un valor medio de 1.49 para el índice de refracción con el cual obtenemos ahora el valor T = .925 aplicando las expresiones utilizadas anteriormente en dicho caso, valor que se corresponde bastante bien con los valores medidos experimentalmente y registrados en el espectro de la figura, que permanecen relativamente constantes en dicho intervalo.
Por el contrario, en la región de longitudes de onda menores de aproximadamente 400 nm la forma del espectro cambia bruscamente y el valor de la transmitancia decrece fuertemente con la longitud de onda, lo cual nos indica que dentro del material existe una fuerte absorción de la radiación con longitudes de onda menores de 400 nm y el material deja de ser transparente para dichas radiaciones, que se puede considerar que pertenecen ya a la región ultravioleta del espectro.
Para radiación de estas longitudes de onda el índice de refracción de este material no se puede seguir considerando que sea real y tendrá una cierta componente imaginaria , N = n - jk , de forma que para valores no muy altos de k , los valores de las transmitancias y reflectancias de las superficies seguirán siendo muy parecidas a las calculadas considerando un índice de refracción real, pero el factor exponencial e-2jd , que resulta al calcular la transmitancia por el método de Airy y que para un índice de refracción real es una función periódica que al integrarse proporciona un valor medio constante independiente de la longitud de onda, ahora tiene una componente exponencial e-4p.k.d /l que afecta al valor de la transmitancia y la hace depender del valor de k y del valor de l.
Por ello, en el caso en que los valores de k son pequeños comparados con el de n, la transmitancia se puede aproximar por la expresión anteriormente utilizada pero afectada ahora por dicho factor exponencial y tendríamos ; T = T1 T2 e-4p.k.d /l /(1- R22), expresión que permitiría hacer una determinación aproximada del índice de absorción , k , en el material del que se ha registrado el espectro de transmisión, si se conoce su espesor y los valores de la transmitancia en una región de no absorción y en la región en la que el material empieza a absorber la radiación, como es el caso en el espectro de la anterior figura.
En efecto, si llamamos T0 a la transmitancia en ausencia de absorción, entonces en la zona en que comienza la absorción y para valores de k no muy altos podremos calcular el valor de dicho índice de absorción como :
-4p.k.d.log(e) /l = log( T /T0 ) => k = l. log( T0 /T ) / ( 4p.d.log(e) )
También a partir de esta expresión es fácil obtener la forma mas conocida de la ley de Bouguer-Beer-Lambert, ya que si T0 = 1 la anterior expresión se convierte en : A = (4p.k.log(e) / l) . d . c = a . d . c , siendo respectivamente ; a = (4p.k.log(e) / l) la llamada absortividad del material en disolución, c la concentración de soluto, que en nuestro caso es 1 o el 100% por haber considerado un material sólido, y d el espesor recorrido por la radiación dentro de la disolución.
La forma en que se consigue que T0 se pueda considerar como la unidad es una técnica utilizada con mucha frecuencia en el análisis químico y que consiste en situar en el haz de referencia de un espectrofotómetro de doble haz una cubeta de idénticas características a la utilizada en el haz de muestra, pero que contenga sólo el disolvente utilizado para disolver la muestra y de esta manera se "compensa" la absorción de fondo debida al disolvente y a la cubeta , o lo que es lo mismo se consigue que el equipo interprete que la transmitancia de la cubeta con el disolvente es 1.
En este tipo de análisis, los espesores de las ventanas de la cubeta y del espacio entre las ventanas, que se llena con la disolución que se quiere medir, son habitualmente mucho mayores que la longitud de coherencia del haz de radiación utilizado en la medida y por ello no se observan efectos de interferencia en los espectros registrados.
Una excepción a este hecho es la que se produce en las medidas realizadas en la región del infrarrojo medio, con longitudes de onda entre 2.5 y 50 micrometros, en cubetas con ventanas de cloruro sódico y pequeños espesores inter-ventana, del orden de 25 o 50 micrometros, en cuyo caso el espesor de fase del espacio entre ventanas es del mismo orden de magnitud que la longitud de coherencia del haz de radiación utilizado y entonces se pueden observar los máximos y mínimos debidos a la interferencia, lo cual se utiliza en algunas ocasiones para determinar con exactitud el espesor útil de la cubeta para su uso en análisis cuantitativos.
Los máximos y mínimos de interferencia se observan también en situaciones en las que la lámina o láminas de material que recubren otros medios tienen un espesor pequeño, del orden de magnitud de la longitud de onda de la radiación incidente y este efecto se observa en muchas ocasiones en la vida cotidiana.
Tal es el caso, por ejemplo, de las finas capas de aceite u otro material menos denso que el agua que se forman sobre la superficie de ésta y que dan lugar a las irisaciones y cambios de color que se observan a veces en charcos de agua o pompas de jabón, que son consecuencia de la interferencia de la luz visible en ellas.
Otro ejemplo que se ve con mucha frecuencia es el de las láminas reflectantes y antireflectantes que se utilizan en aplicaciones tales como los cristales "espejo" que se usan para conseguir mayor opacidad en uno de los sentidos de la visión y los de las lentes antireflectantes de uso oftalmológico, respectivamente.
También se utilizan con mucha frecuencia materiales en forma de lámina delgada para usos en el campo de la electrónica y de la generación de energia eléctrica fotovoltaica y en este caso también es posible obtener información sobre las propiedades de los materiales utilizados, a partir de medidas de transmisión o reflexión realizadas sobre dichos materiales.
En las medidas de transmisión y reflexión se usan los valores de longitud de onda a la que se producen los máximos y mínimos de interferencia y las lecturas de transmitancia o reflectancia en dichos puntos para determinar el espesor y el índice de refracción de materiales que se utilizan en forma de lámina delgada depositada sobre otra lámina de material de mayor espesor y capacidad portante.
Este es el caso de la figura que se presenta a continuación en la que se puede ver el registro gráfico de la medida de la transmitancia de una lámina delgada de sulfuro de cadmio (CdS) depositada sobre una lámina de vidrio de 100 mm de espesor, de las utilizadas como cubreobjetos en los microscopios (21).
El ancho de banda de la radiación utilizada se ha mantenido en 2 nm y el rango de longitudes de onda explorado ha sido de 400 nm a 850 nm, habiendo sido el tiempo empleado en registrarlo de un minuto aproximadamente.

A partir del espectro de transmisión de la figura se leen los valores de transmitancia, T=0.68 en el mínimo a 787.5nm y T=0.85 en el máximo a 811.1nm y utilizando un método como el descrito en (7) se llegan a obtener el orden de interferencia, m=16 , el espesor de la lámina, d=3.06mm , su índice real de refracción a las dos longitudes de onda , n(l1)=2.120 , n(l2)=2.118 , y el coeficiente de absorción k=1.53 .10-3 en el máximo de transmitancia. El cálculo de estos valores se ha hecho de forma automatizada empleando el programa de cálculo de índices de refracción y espesores que se puede utilizar en linea en (22).
En este caso la longitud de coherencia del haz de radiación es comparable con el espesor óptico de la lámina de vidrio usada como substrato y por tanto deberían aparecer en el espectro registrado algunos efectos de interferencia, debidos al mismo, superpuestos con los efectos de interferencia de la lámina delgada de CdS, pero en el anterior espectro no se aprecian.
La causa de ello hay que buscarla en el tipo de registro realizado, que no tiene la suficiente resolución entre punto y punto como para reflejar las pequeñas oscilaciones que deberían observarse. Para visualizar este efecto con más claridad se han realizado otros dos registros de la misma lámina y substrato, esta vez con mayor resolución gráfica, uno con el mismo ancho de banda anterior, 2 nm, y otro disminuyendo el ancho de banda experimental hasta 0.5 nm.
Los registros se han hecho ahora entre 550nm y 850nm y el resultado puede verse en las imágenes siguientes:
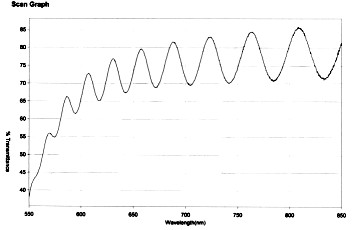 |  |
Ahora sí se observan en los dos registros las oscilaciones debidas a la interferencia dentro del sustrato de vidrio, aunque el efecto se hace más evidente cuando se reduce el ancho de banda de la radiación utilizada y cuanto mayor es la longitud de onda y, por tanto, la longitud de coherencia del haz de radiación.
En (22) también se puede encontrar un programa con el que es posible realizar la simulación de los espectros de transmisión y reflexión completos para sistemas de hasta 8 láminas de cualquier espesor, en todo el rango de longitudes de onda, con anchos de banda variables, para cualquier ángulo de incidencia y diferentes tipos de polarización de la radiación incidente.
Utilizando este programa se ha hecho una simulación del espectro de transmisión y reflexión de la lámina de CdS sobre substrato de vidrio, cuyo espectro de transmisión se presentó en la anterior figura, para lo cual se han utilizado los valores de espesor e índice de refracción encontrados, se ha ajustado el índice de refracción a una sencilla expresion polinómica del tipo : n = 2.1 - .043/l + .046/l2 y el coeficiente de absorción a una expresión lineal del tipo ; k = .1514 - .245l , en el tramo de longitudes de onda entre 520nm y 600nm y de ; k = .0212 - .028l , entre 600nm y 700nm, expresiones que se han encontrado para este caso concreto a partir del espectro de transmisión registrado y con las cuales se han obtenido los espectros calculados, usando anchos de banda de 2 nm y 1.5 nm respectivamente, que se ofrecen en las siguientes figuras.
 |  |
En estas simulaciones se observan también los efectos de interferencia del sustrato superpuestos a los de la lámina de CdS y su dependencia con el ancho de banda usado en la simulación y con la longitud de onda de la radiación, al igual que se observaba en los espectros de transmisión registrados experimentalmente.
Dicho ancho de banda utilizado en la simulación se ha tomado como la anchura de una distribución rectangular de las intensidades de radiación dentro del haz incidente, y la similitud entre las curvas calculadas y las obtenidas experimentalmente es bastante satisfactoria, como puede observarse al comparar las anteriores figuras, si se tiene en cuenta la diferencia de expansión de los ejes de ordenadas en uno y otro caso.
Se observa también que en estas simulaciones realizadas, los efectos de interferencia producidos en el substrato son más acusados que los que se observan en los espectros registrados experimentalmente y este hecho puede explicarse por las limitaciones que tiene el registro experimental en cuanto a la resolución gráfica de dicho registro y otros efectos espúreos de integración que se producen de forma involuntaria sobre el mismo, mientras que dichos efectos están ausentes en el caso de los espectros calculados.
Otra de las características que tiene mucha influencia sobre la transmitancia y reflectancia medidas es la rugosidad superficial de la o las interfases entre los medios, siendo habitualmente la de la primera interfase la que es más significativa, al ser la cantidad de radiación dispersada fuera de la dirección especular dependiente de la diferencia de los índices de refracción de los medios a uno y otro lado de la interfase rugosa, así como de las características de la rugosidad superficial.
En el caso de las medidas de reflexión en superficies rugosas de medios muy reflectantes, como es el caso de los metales, la radiación desviada fuera de la dirección especular es función del ángulo de incidencia y de las características de la rugosidad de la superficie y los índices de refracción de los medios a uno y otro lado de la interfase, mientras que en el caso de las medidas de transmisión o reflexión en medios poco reflectantes, como es el caso de los dieléctricos, dicha radiación desviada fuera de la dirección predicha por las leyes de Snell dependerá también de los espesores y características de las láminas que la radiación deba atravesar después de pasar la superficie con rugosidad.
Por ello, en muchas ocasiones sucede que una fracción de la radiación que alcanza el detector es radiación que en parte ha sufrido difracción en la rugosidad superficial, pero que ha sido redirigida a dicha dirección tras sufrir diversas desviaciones y por ello, es a la radiación que alcanza el detector dentro de un pequeño ángulo de apertura a la que se hace referencia cuando se habla de radiación transmitida o reflejada en la dirección especular.
En el caso de superficies muy lisas, con poca rugosidad superficial, la radiación reflejada y trasmitida lo será de acuerdo con las leyes de Snell y además será radiación que mantiene la coherencia de la fase, al no haber sufrido difracción, por lo cual puede verse reflejada en ellas o transmitida a través suyo la forma y características de los objetos que están delante o detrás, respectivamente.
En el caso opuesto, de superficies con rugosidad superficial grande, la radiación reflejada y transmitida en ellas ha sufrido difracción y por tanto ha perdido la coherencia de fase, por lo cual no podremos observar la forma o características de los objetos delante o detrás de ellas y lo que observaremos será la imagen formada por la difracción en las facetas de la superficie.
Entre uno y otro extremo puede haber toda una gama de situaciones intermedias en las que las superficies pueden resultar mas o menos transparentes y reflejar de forma más o menos distorsionada dependiendo de las propiedades concretas de la superficie y material considerados, pero es remarcable que en la Naturaleza la mayoría de las superficies presentan grados de rugosidad considerables y sólo en algunos pocos casos se pueden observar superficies relativamente lisas, como es el caso de los cristales, las superficies de fluidos en reposo y algunas pocas mas.
Para observar el efecto que tiene un cierto grado de rugosidad superficial sobre la radiación transmitida en la dirección especular, se ha producido una rugosidad sobre la lámina de polimetil-metacrilato cuyo espectro de transmisión se vió anteriormente y se ha vuelto a registrar el espectro de transmisón de la lámina, manteniendo un pequeño ángulo de aceptación del detector para que la radiación recogida sea la que se transmite en la misma dirección que la de incidencia, y pueda considerarse que la transmitancia registrada es la especular.
Los dos espectros se pueden ver en la figura siguiente, en la que se observa una disminución de la transmitancia especular para la lámina con superficie rugosa con respecto a la de superficie lisa y que dicha disminución tiene dependencia con la longitud de onda, siendo la transmitancia menor para longitudes de onda más pequeñas.
 |  |
La rugosidad que se ha producido en la superficie de la lámina no ha sido controlada y podría ser similar a la que se produciría en una lámina de estas características que esté expuesta, por ejemplo, a los agentes atmosféricos y al desgaste producido en la misma debido a su uso en paneles o ventanas exteriores.
La rugosidad no es muy grande pero confiere un cierto aspecto "lechoso" a la superficie, produciendo una disminución de la visibilidad a través de la lámina, lo cual se aprecia de forma cuantitativa en su espectro de transmisión.
La simulación numérica de estos dos casos, lámina de 3 mm de espesor con superficie lisa y la misma lámina en la que se ha producido rugosidad en la primera superficie, se ha realizado utilizando un programa que incluye el modelo para superficies rugosas que se vió en el apartado de superficies lisas y rugosas, y que está disponible en (22).
En la figura siguiente se ofrece el resultado de la simulación numérica de los dos espectros, en el que la parte real del índice de refracción se ha tomado igual a 1.49 en todo el rango de longitudes de onda y la parte imaginaria se toma como k=0 entre 400nm y 800nm, se ajusta a la recta k=(0.4125-1.0313.l).10-3 en el tramo entre 368nm y 400nm y se toma como k=4.10-3 para longitudes de onda menores que 368nm.
Los valores que se han tomado para la rugosidad superficial en la simulación han sido h=120nm para la altura máxima de las desviaciones y a=120nm para la distancia media de correlación entre ellas, por lo que el modelo de la superficie rugosa utiliza una sola capa para representar la superficie, y el valor del parámetro b se toma igual a 0.
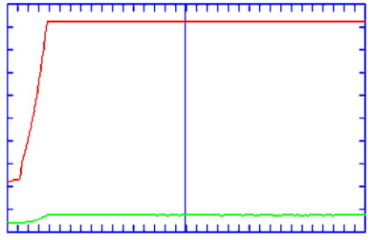 | 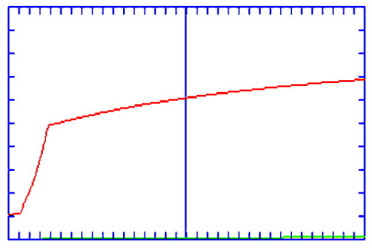 |
Comparando estas simulaciones con los registros obtenidos experimentalmente se observa que en la zona de absorción, entre 350nm y 400 nm los valores de transmitancia medidos y calculados siguen la misma tendencia aunque parece que se habrían ajustado mejor a una dependencia de k con l1/2 en lugar de la lineal con l que se ha utilizado en la simulación, mientras que en la región de longitudes de onda comprendidas entre 400nm y 800nm, en la que el índice de absorción se toma como cero y por tanto la disminución de el valor de la transmitancia es sólo atribuible al efecto de la rugosidad superficial, el acuerdo entre los valores medidos y los calculados es aceptablemente bueno por lo que el método utilizado se puede considerar válido en este caso para tener en cuenta los efectos de la rugosidad superficial sobre la radiación transmitida por la lámina.
En la simulación realizada se han calculado también los valores de la reflectancia especular en ambos casos, superficie lisa y rugosa, y se puede ver que la disminución de la reflectancia especular que se aprecia entre uno y otro caso explica la apariencia que presenta la superficie con rugosidad en la que la reflexión corresponde mayoritariamente a radiación difusa y no se produce prácicamente ninguna o muy poca reflexión especular.

Referencias
1.- Magnitudes, Unidades y Símbolos en Química Física. IUPAC , 1993.
2.- V.V. Nikolski, en Electrodinámica y propagación de ondas de radio. Editorial Mir. Moscú, 1976.
3.- J.R. Reitz, F.J. Mildford, S.B. Perelberg, en Fundamentos de la teoría electromagnética. Editorial UTEHA. México,D.F. 1972.
4.- J.A. Stratton, en Electromagnetic theory. Editorial McGraw-Hill. N.York-London, 1941.
5.- Z. Knittl, en Optics of thin films. Editorial John Wiley & Sons, London-N.York, 1976.
6.- Grupo de Innovación Docente en Óptica Física y Fotónica. Departamento de Física Aplicada y Óptica. Universidad de Barcelona, en Javaoptics.
7.- F.Valcarce, M.Rodriguez Vidal, en Interpretación de medidas de transmisión óptica en láminas delgadas plano-paralelas, Anales de Física, B, vol.77, 1981.
8.- A.N.Zaidel, G.V.Ostróvskaya, Yu.I.Ostrovski, en Técnica y práctica de espectroscopía. Editorial MIR. Moscú, 1979.
9.- M.Born, E.Wolf, en Principles of Optics. Editorial Pergamon Press. Oxford, 1980.
10.- P.H. Berning, en Physics of thin films I, chapter III. Editorial Academic Press. New York, 1963.
11.- H.E.Bennett, J.O.Porteus en Relation between surface roughness and specular reflectance at normal incidence. J. of the Optical Society of America, 51, 2, 1961.
12.- P.Beckmann, A.Spizzichino, en The scattering of electromagnetic waves from rough surfaces. Editorial Pergamon Press, The macmillan company, N.York, 1963.
13.- I. Filinski, en The effects of sample imperfections on optical spectra, Physics status solidii (b) 49, 1972.
14.- N.A.Voishvillo, L.D.Blinova en Using milk glass to produce fields of uniform ilumination. , Sov.J.Opt.Technol.49, 1982.
15.- S.Craig, G.L.Harding en Solar selective properties of rough sputtered cooper films, Solar energy materials, 4, 1981.
16.- H.B.Stephens, G.D.Cody en Optical reflectance and transmission of a textured surface, Proc. International Conference on metallurgical coatings, San Francisco, Cal., 1977.
17.- F.Valcarce, M.Rodriguez Vidal, en Reflexión y transmisión ópticas en láminas delgadas con superficie rugosa, Proc. XIX Reunión Bienal de la Real Sociedad Española de Física y Química, Santander, 1982.
18.- Beckman Instruments GmbH, en Instruction Manual for the Beckman Model DU, München, 1960.
19.- Perkin-Elmer Corporation, en Microprocesor double monochromator UV-VIS-NIR spectrophotometer, Instrument News, vol.27, nº1, 1977.
20.- S.Nikolova Kasarova, N.Georgieva Sultanova, C. Dimitrov Ivanov and I. Dechev Nikolov, en Analysis of the dispersion of optical plastic materials, Optical Materials, Vol. 29, nº11, 2007.
21.- F. Valcarce, en Influencia de la presión del gas de la descarga en las características de laminas delgadas de CdS crecidas por pulverización R.F. Análisis por transmisión óptica. Informe al Dpto. de Electricidad. y Electrónica, Facultad CC. Físicas, Universidad Complutense de Madrid. 1981.
22.- http//:webs.ono.com/fvcg/publi/programas/programas.htm. Área de programas de Ciencia y Tecnología.


|